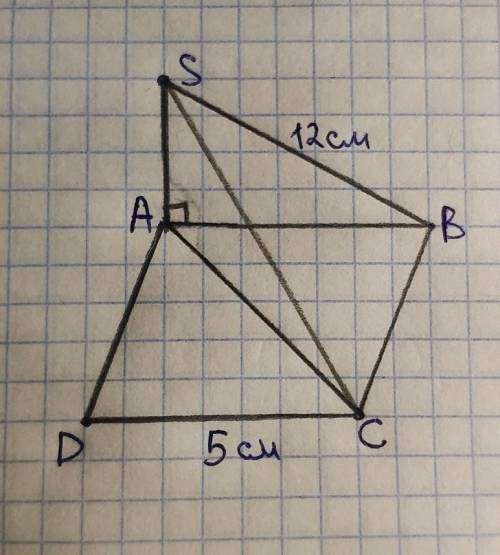
Все стороны квадрата равны. АВСD – квадрат по условию, тогда AD=AB=CD=5 см.
Углы квадрата прямые, то есть угол ADC=90°, следовательно ∆ADC – прямоугольный.
В прямоугольном треугольнике ASC по теореме Пифагора:
AC²=AD²+CD²
AC²=5²+5²
АС²=25+25
АС=√50 см
Если прямая перпендикулярна плоскости, значит она перпендикулярна всем прямым, лежащим на этой плоскости. Исходя из этого: так как SA перпендикулярна АВСD, то угол SAB=угол SAC=90°.
Так как угол SAB=90°, то ∆SAB – прямоугольный.
В прямоугольном треугольнике SAB по теореме Пифагора:
SB²=SA²+AB²
12²=SA²+5²
144=SA²+25
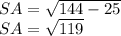
Так как угол SAC=90°, то ∆SAC – прямоугольный.
В прямоугольном треугольнике SAC по теореме Пифагора:
SC²=SA²+AC²
SC²=(√119)²+(√50)²
SC²=119+50
SC²=√169
SC=13 см.
ответ: 13 см.
Дано:
АВСЕ — параллелограмм,
АВ = 8 сантиметров,
периметр АВСЕ равен 36 сантиметров.
Найти длины сторон параллелограмма АВСЕ: СЕ, ВС, АЕ — ?
Рассмотрим параллелограмм АВСЕ. У него противолежащие стороны равны между собой, тогда ВС = АЕ , АВ = СЕ = 8 сантиметров.
Р АВСЕ = АВ + СЕ + ВС + АЕ;
36 = 8 + 8 + ВС + ВС;
36 = 16 + 2 * ВС;
36 - 16 = 2 * ВС;
20 = 2 * ВС;
ВС = 20 : 2;
ВС = 10 сантиметров.