Чертеж к решению - во вложении.
Известно, что биссектрисы двух непротивоположных углов параллелограмма пересекаются под прямым углом и отсекают равнобедренные треугольники. Таким, образом, треугольники АВК и МСД равнобедренные, а треугольник КРМ - прямоугольный.
Все равные углы (накрест лежащие и вертикальные), а также равные отрезки отмечены на чертеже.
Ведем обозначения: ВК=КМ=МС=х, КР=у, МР=z.
Периметр параллелограмма P=2(АВ+ВС)=8х.
Треугольники РАД и РКМ подобны по двум углам. Поэтому
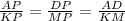
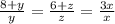
1) 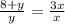
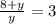
3y=8+y
y=4,
2) 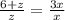
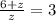
z+6=3z
z=3,
По теореме Пифагора в треугольнике КРМ
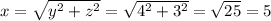
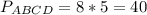
ответ: 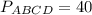
Пирамида правильная, значит в основании квадрат. Обозначим пирамиду SАВСД. S -вершина. Проведём диагонали АС и ВД. В квадрате диагональ равна (а корней из2). Где а -сторона квадрата. По условию а=1,тогда АС=ВД= корень из 2. Расстояние между SВ и АС это перпендикуляр ОК из точки пересечения диагоналей О к ВS. Рассмотрим треугольник SВО( можно нарисовать отдельно). Это прямоугольный треугольник, у которого гипотенуза SВ=1(ребро пирамиды), катет ВО=ВД/2=(корень из 2 )/2. Второй катет SО это высота пирамиды. SО= корень из (ВSквадрат-ВОквадрат)=корень из (1-2/4)=(корень из 2)/2. Площадь треугольника Ssво=1/2*ВО*SО, она также равна Ssво=1/2*ВS*ОК. Приравнивая оба этих выражения, получим 1/2*(корень из 2)/2*(корень из 2)/2=1/2*1*ОК. Отсюда искомое расстояние ОК=1/2.