Объяснение:
Дано:
Отрезок с концами в точках N (-2; 3) и K (3 - 4). в
Выполните:
а) параллельный перенос отрезка NK, заданный вектором a (-5; 4);
б) поворот отрезка NK вокруг точки К на 60 ° против часовой стрелки
Решение.
a)
При параллельном переносе отрезка NK с . вектора a координаты отрезка N'K' равны
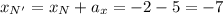
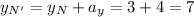
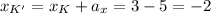
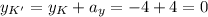
то есть в результате параллельного переноса получили отрезок N'K' c концами N'(-7; 7) и K' (-2; 0)
б)
Осуществим такой параллельный перенос системы координат, при котором начало координат находится в точке К
В новой (Х,У) системе координат координаты точки N равны
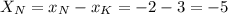
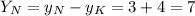
Теперь повернём вектор KN (-5; 7) вокруг точки К на угол α = 60°
Поворот на плоскости задаётся формулами
x' = x · cos α + у · sin α
y' = x · sin α + y · cos α
Поэтому координаты точки N' будут равны
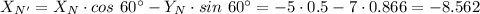
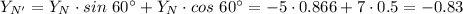
В начальной системе координат (х,у) координаты точки N'
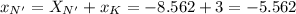
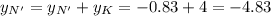
Таким образом. в результате поворота отрезка NK вокруг точки K на угол α = 60° против часовой стрелки получили отрезок N'K c концами в точках N'(-5.862; -4.83) и К(3; -4)
Назовем трапецию АВСД, где ВС и АД - основания. Из т.С опустим перпендикуляр СЕ к стороне АД. АВСЕ - прямоугольник по построению, значит АЕ=ВС=3. ЕД=АД-АЕ=5-3=2.
Из треугольника СДЕ: угол ДСЕ=180-СЕД-СДЕ=180-90-45=45. Значит треугольник СДЕ равнобедренный, значит СЕ=ЕД=2
СД^2=CE^2+EД^2=2^2+2^2=8, СД=2*корень из 2
Тело вращения представляет собой объединение цилиндра с осью АЕ и конуса с осью ДЕ.
S(боковая конуса) = пи*R*L=пи*СЕ*СД=3,14*2*2*корень из 2=12,56*корень из 2
S(боковая цилиндра) = 2*пи*R*ВС=2*пи*СЕ*ВС=2*3,14*2*3=37,68
S(основания)=пи*R^2=пи*СЕ^2=3,14*2^2=12,56
Все складываем и получаем
S=50,24+12,56*(корень из 2)
Відповідь:
Пояснення:
1) AB = BC/cos B = 2/(2/3) = 3;
sin B =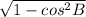 =
= 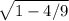 =
= 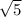 / 3;
/ 3;
AC = AB *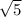 /3 = 3 *
/3 = 3 * 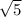 /3 =
/3 = 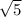 .
.
Або можна використати для обчислення третьої сторони теорему Піфагора: AC = =
=  =
= 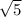 .
.
Надалі для обчислення третьої сторони використовуватиму теорему Піфагора.
2) AB = AC/sin B = 3/(1/4) = 12;
BC =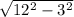 =
= 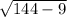 =
= 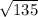 = 3
= 3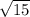 .
.
3) BC = AC*ctg B = 4*2 = 8;
AB =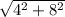 =
= 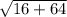 =
= 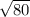 = 4
= 4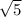 .
.
4) AC = AB*cos A = 8*(5/8) = 5;
BC = =
= 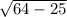 =
= 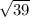 .
.
5) AB = AC/sin A = 2/(3/5) = 10/3;
BC =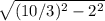 =
= 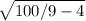 =
= 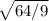 = 8/3.
= 8/3.