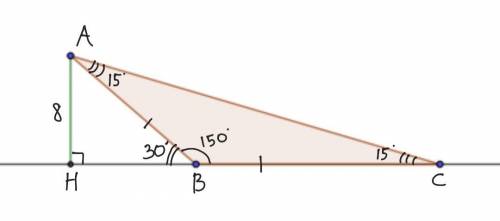
Дано: ΔABC - равнобедренный, АС - основание, АВ=ВС, ∠В=150°, АН - высота, АН = 8 е.д.
Найти: BC.
Решение.
Поскольку треугольник тупоугольный, а высота проведена из острого угла, то высота принадлежит продолжению противолежащей стороны.
Поэтому рисуем продолжение прямой ВС и высоту АН, проведённую к нему.
В ΔАНВ: ∠НВА = 180°-150°= 30° (как смежные).
АНВ - прямоугольный треугольник (АН ведь высота) с гипотенузой АВ.
В прямоугольном треугольнике, если острый угол равен 30°, то противолежащий этому углу катет равен половине гипотенузы.
АН=½АВ.
АВ= 2АН.
АН по условию 8, тогда АВ= 2×8=16.
ΔАВС - равнобедренный, АВ=ВС. Значит, ВС=16 е.д.
ответ: 16 е.д.
Відповідь:
LМ = 22,8 см.
ЕК = 45,6 см.
Периметр ОLМ = 68,4 см.
Пояснення:
Хорда LМ и диаметр ЕК перпендикулярны
LМ = LА × 2 = 11,4 × 2 = 22,8 см.
Диаметр ЕК равен длине двух хорд LМ равных радиусу
ЕК = LМ × 2 = 22,8 ÷ 2 = 45,6 см.
Треугольник ОLМ - равносторонний LМ = МО = ОL
Р = 22,8 × 3 = 68,4 см.