1) Сумма внешнего и внутреннего угла многоугольника равна 180° ⇒ следовательно внутренний угол многоугольника равен 180° - 20° = 160°
Величина внутреннего угла правильного многоугольника зависит от количества его сторон n и выражается формулой:
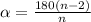
Найдем при каком n угол будет равен 160°:
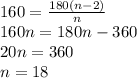
Т.е. угол в 160° будет у правильного 18-угольника
2) Радиус окружности описанной около правильного треугольника R и сторона a треугольника связаны соотношением:
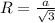
Подставим заданное значение стороны:
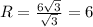
Следовательно, радиус окружности, описанной около этого треугольника равен 6 см
3) Градусная мера всей окружности равна 360°, а радианная мера 2π, следовательно градусная мера дуги равна:
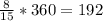 °
°
а радианная:

Длину дуги найдем как 8/15 от длины окружности:
 см
см
r=7.5 cm
Объяснение:
Пусть дан прямоугольный треугольник АВС, в котором угол В-прямой. Окружность с центром в точке О, которая лежит на гипотенузе касается катета ВС в точке Т и проходит через точку А. Гипотенуза АС пересекает окружность в точке К. К находится между О и А.
Известно, что катеты АВ=12 и ВС=16.
Проведем радиус ОТ. Так как Т точка касания , то треугольник ОТС-прямоугольный и угол Т -прямой.
Косинус угла С равен:
cosC=BC/AC
Найдем АС по т. Пифагора из треугольника АВС:
АС=sqr(AB^2+BC^2)=sqr(144+256)=sqr400=20
cosC=16/20=4/5
sinC =sqr(1-cosC^2)=sqr(1-16/25)=sqr(9/25)=3/5
ОС=ОТ/sinC=r*5/3=OK+KC
5/3*r=r+KC
KC=2/3*r
AC=20=2r+2/3*r
8*r/3=20
8r=60
r=60/8
r=7.5 cm