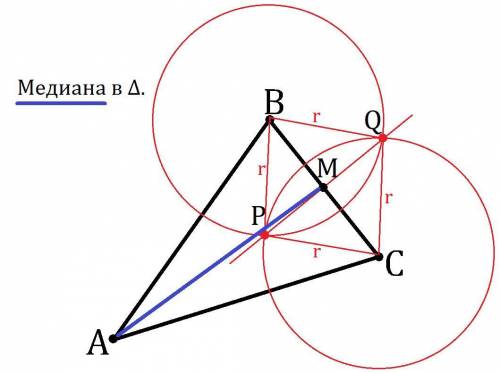
Медиана треугольника соединяет вершину треугольника и середину противоположной стороны, значит чтобы построить медиану нам нужно найти середину стороны. Пусть в ΔABC мы хотим провести медиану из вершины A на сторону BC, для этого:
Из точек B и C проводим с циркуля окружности с одинаковым радиусом r, при этом r зрительно больше половины BC (можно взять r = BC). Окружность пересекутся в двух точка Q и P, проводим с линейки прямую QP, QP∩BC = M, это и будет середина BC.
Это правда, потому что у четырёхугольника BQCP все стороны равны r, поэтому это ромб, а у ромба диагонали делятся точкой пересечения пополам.
Теперь с линейки соединяем точки A и M, полученные отрезок AM и будет медианой.
Как расположены точки А(-2; 6), В(-6; 1) относительно окружности
(х + 2)² + (у – 1)² = 36
Объяснение:
Подставим координаты точки в левую часть уравнения
А(-2; 6), (-2 + 2)² + (6 – 1)² =0+25 =25 ; тк 25<36, то внутри окружности.
В(-6; 1), (-6 + 2)² + (1 – 1)² =16+0 =16 ; тк 16<36, то внутри окружности.