Объяснение:
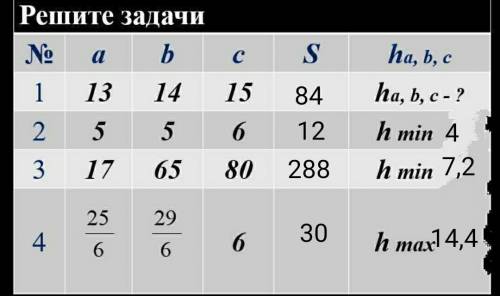
1)
p=(a+b+c)/2=(13+14+15)/2=21см полупериметр
S=√(p(p-a)(p-b)(p-c))=√(21*8*7*6)=√7056=
=84см² площадь треугольника
h(a)=2S/a=2*84/13=168/13=12цел12/13 см
h(b)=2S/b=168/14=12 см
h(c)=2S/c=168/15=11,2 см.
ответ: площадь 84см²; высота проведенная к стороне а равна 12цел12/13см.; высота проведенная к стороне b равна 12см; высота проведенная к стороне с равна 12,2см.
2)
p=(a+b+c)/2=(5+5+6)/2=8см полупериметр
S=√(8(8-5)(8-5)(8-6))=√(8*3*3*2)=√144=
=12 см² площадь треугольника.
h(min)=2S/c=2*12/6=24/6=4см самая маленькая высота.
ответ: S=12см²; h(min)=4см.
3)
р=(а+b+c)/2=(17+65+80)=162/2=81см полупериметр треугольника.
S=√(81*64*16*1)=√82944=288см²
h(min)=2S/c=2*288/80=7,2см высота.
ответ: S=288см²; h(min)=7,2 см высота.
4)
р=(25/6+29/6+36/6)/2=90/6*1/2=45/6см полупериметр.
S=√(45/6*20/6*16/6*9/6)=√129600/√1296=360/12=30см². площадь треугольника
h(max)=2S/a=60:25/6=60/1*6/25=14,4 см максимальная высота
ответ: S=30см²; h(max)=14,4см.
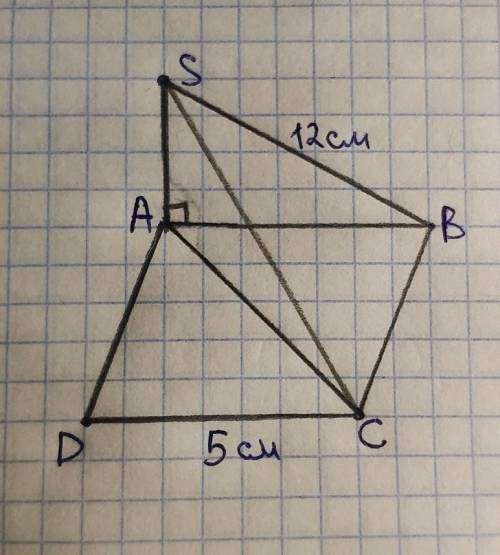
Все стороны квадрата равны. АВСD – квадрат по условию, тогда AD=AB=CD=5 см.
Углы квадрата прямые, то есть угол ADC=90°, следовательно ∆ADC – прямоугольный.
В прямоугольном треугольнике ASC по теореме Пифагора:
AC²=AD²+CD²
AC²=5²+5²
АС²=25+25
АС=√50 см
Если прямая перпендикулярна плоскости, значит она перпендикулярна всем прямым, лежащим на этой плоскости. Исходя из этого: так как SA перпендикулярна АВСD, то угол SAB=угол SAC=90°.
Так как угол SAB=90°, то ∆SAB – прямоугольный.
В прямоугольном треугольнике SAB по теореме Пифагора:
SB²=SA²+AB²
12²=SA²+5²
144=SA²+25
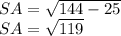
Так как угол SAC=90°, то ∆SAC – прямоугольный.
В прямоугольном треугольнике SAC по теореме Пифагора:
SC²=SA²+AC²
SC²=(√119)²+(√50)²
SC²=119+50
SC²=√169
SC=13 см.
ответ: 13 см.
Відповідь:
45°
Пояснення:
Застосуємо теорему синусів