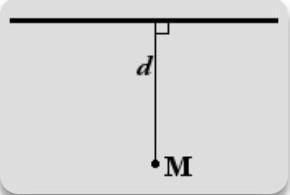
Определение. Расстояние от точки до прямой
равно длине перпендикуляра, опущенного из точки на прямую
Объяснение:
Если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(Mx, My) до прямой можно найти, используя следующую формулу
d = |A·Mx + B·My + C|
√A2 + B2
● Найти расстояние между прямой 3x + 4y - 6 = 0 и точкой M(-1, 3).
Решение. Подставим в формулу коэффициенты прямой и координаты точки
d = |3·(-1) + 4·3 - 6| = |-3 + 12 - 6| = |3| = 0.6
√32 + 42 √9 + 16 5
ответ: расстояние от точки до прямой равно 0.6.
думаю так;)
Осевое сечение конуса - это равнобедренный треугольник. Следовательно, угол при вершине делится высотой конуса пополам. Тогда в прямоугольном треугольнике, образованном высотой конуса, его радиусом (катеты) и образующей (гипотенуза) Образующая L=2R, так как радиус лежит против угла 30°. Учитывая, что R = (2-L) см (дано), можем написать: L =2*(2-L) см. => L=4-2L, => L=4/3 см.
Тогда R=2/3 см.
Площадь полной поверхности конуса равна сумме площадей основания и боковой поверхности, то есть S = So +Sб, или S=π(R²+R*L). подставляя найденные значения, получим
S = π(4/9+2*4/(3*3)) = 12/9 = 4/3см² = 1и1/3 см².
ответ: S=1и1/3 см².
1) Концы отрезка А(3; 1; 8) и В (5; 7; 2). Найдите точку, симметричную середине отрезка относительно плоскости xОz.
Пусть О-середина АВ, тогда
х(О)=(3+5):2=4,
у(О)=(1+7):2=4,
z(О)=(8+2):2=5 ⇒ О(4 ; 4 ;5).
Точка, симметричная т.О относительно плоскости xОz имеет координаты
(4 ; - 4 ; 5).
2) Точки А (4; 2; 10), B(10; -2; 8), С(-2; 0; 6) — вершины параллелограмма ABCD. Найдите координаты вершины D.
Точка D может быть получена параллельным переносом точки C на вектор BA . Вектор ВА= CD.
Вектор BA( 4-10 ; 2+2 ;10-8 ) или
ВА( -6 ; 4 ; 2 )
х(D)=x(C)+x(BA) ⇒ х(D)=-2+(-6)=-8 ,
y(D)=y(C)+y(BA) ⇒ y(D)= 0+4= 4 ,
z(D)=z(C)+z(BA) ⇒ z(D)=6 + 2=8 .
Тогда D (-8 ; 4; 8).