6 ед.
Объяснение:
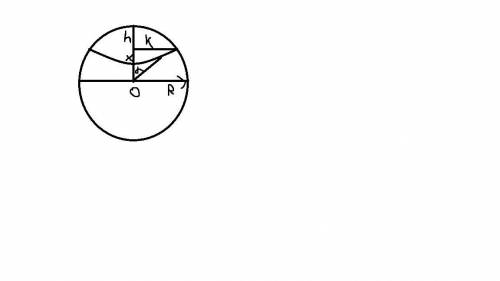
В правильной усеченной пирамиде в основаниях лежат правильные многоугольники, стороны которых соответственно равны между собой. Боковые грани такой пирамиды - равные между собой равнобокие трапеции. Радиусы окружностей, вписанных в основания, проведенные в точки касания сторон оснований с соответственной окружностью Н и Н1, перпендикулярны к сторонам оснований по свойству радиусов, проведенных в точки касания.
Проведем перпендикуляр из точки касания Н1М верхнего основания на нижнее основание. Тогда отрезок Н1Н перпендикулярен стороне основания АВ по теореме о трех перпендикулярах, то есть является искомой высотой боковой грани.
В прямоугольном треугольнике НН1М угол ∠НН1М = 30° по сумме острых углов. Следовательно, НН1 = 2·НМ по свойству катета, лежащего против угла 30°.
НМ = ОН - О1Н1 = 8-5 = 3 ед.
Высота боковой грани НН1 = 6 ед.
ответ: 8м
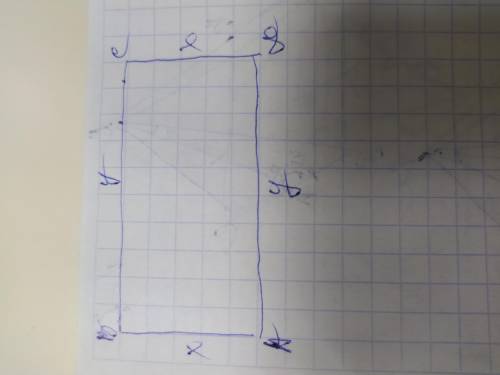
Объяснение: пусть одна сторона=х, а вторая =у. Составим систему уравнений используя формулу площади прямоугольника и формулу его периметра: Р=2(х+у)
S=xy
Подставим в уравнение известные нам значения:
2(х+у)=32 |÷2
ху=64
х+у=16
ху=64
х=16-у
Теперь подставим значение х во второе уравнение: ху=64
(16-у)у=64
16у-у²=64
-у²+16у-64=0 |×(-1)
у²-16у+64=0
(у-8)²=0
у-8=0
у=8
Одна сторона=8м
Теперь подставим значение у в первое уравнение: х=16-у=16-8=8м
Наш прямоугольник является квадратом, у которого все стороны равны
Sсег=200π-100π√3
V=4000π/3
Объяснение:
1)
cos<альфа=х/R
cos30°=√3/2
√3/2=x/10
x=10√3/2=5√3.
h=R-x=10-5√3
Sегм=2πRh=2π*10*(10-5√3)=20π(10-5√3)=
=200π-100π√3
2)
V=4πR³/3=4π*10³/3=4000π/3