г) 7,5 см.
Объяснение:
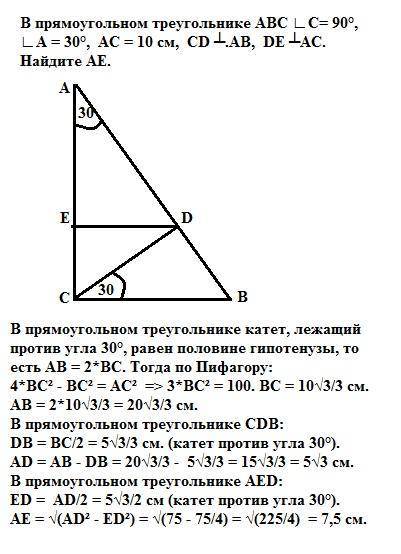
В прямоугольном треугольнике катет, лежащий против угла 30°, равен половине гипотенузы, то есть АВ = 2*ВС. Тогда по Пифагору:
4*ВС² - ВС² = АС² => 3*ВС² = 100. ВС = 10√3/3 см.
AB = 2*10√3/3 = 20√3/3 см.
В прямоугольном треугольнике CDB:
DB = BC/2 = 5√3/3 см. (катет против угла 30°).
AD = AB - DB = 20√3/3 - 5√3/3 = 15√3/3 = 5√3 см.
В прямоугольном треугольнике AED:
ED = AD/2 = 5√3/2 см (катет против угла 30°). Тогда по Пифагору:
AE = √(AD² - ED²) = √(75 - 75/4) = √(225/4) = 7,5 см.
Объяснение:
Треугольник FAC и его ортоцентр - это центр вписанной окружности треугольника ABC
Объяснение: Автор задания не совсем удачно обозначил центры вписанной и описанной окружностей. Обычно центр вписанной окружности - это точка I, центр описанной - точка O.
С разрешения автора буду считать, что центр вписанной окружности - это I. Кстати, картинка не совсем удачная. Дело в том, что, как известно, на одной прямой (прямой Эйлера) находятся центр O описанной окружности, центроид (то есть точка G пересечения медиан) и ортоцентр H. Центр же вписанной окружности лежит на этой прямой только если треугольник равнобедренный. Перехожу к решению.
Каждый из углов тр-ка ABC будем обозначать одной буквой - A, B, C. Значок градуса будем опускать. Из равнобедренного тр-ка EAC имеем: угол ECA=90-(A/2); из равноб. тр-ка ACD имеем: CAD=90-(C/2). Поэтому AFC=(A+C)/2. I лежит на биссектрисе угла BAC, то есть IAC=A/2, откуда DAI=DAC-IAC=90-(A+C)/2. То есть AFC+FAI=90, откуда AI перпендикулярно FC. Аналогично CI перпендикулярно AF. Следовательно, центр вписанной окружности треугольника ABC является по совместительству - ортоцентром треугольника FAC.