Посмотрите предложенный вариант: В 4-угольнике стороны образуют прямые углы. 1. Тогда необходимо доказать, что |KL|⊥|LM|; |LM|⊥|MN|; |MN|⊥|KN|. Для этого можно либо вычислить косинус угла между векторами, либо составить уравнения прямых, проходящих через эти пары точек. Решение вторым 2. Для нахождения уравнения прямой необходимо составить два линейных уравнения и решить их как систему. Решение показано во вложении. 3. Из полученных уравнений для прямых видно, что а) KL || MN, LM || KN; (коэффициенты при Х равны) b) KL⊥LM (⊥KN); LM⊥MN (⊥KL) (произведение коэффициентов при Х даёт (-1).
АВ=ВС=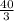 ,
,
АС=
Объяснение:
ΔАВС. АВ=ВС, АВ:АС=2:5
Пусть АВ=ВС=2х, АС=5х,
Периметр = АВ+ВС+АС = 2х+2х+5х=60
9х=60
х=60/9=20/3
АВ=ВС=2* 20/3 = 40/3
АС=5х=5* 20/3 = 100/3