Доказательство:
Так как треугольник остроугольный и BD - биссектриса, то ∠B<90°⇒∠CBD<45°=∠DFC, следовательно F∈BC.
Проведем из точки D перпендикуляр до отрезка BC с основанием M, M будет принадлежать стороне BC поскольку треугольник остроугольный.
Тогда прямоугольные треугольники BDE и BDM равны по общей гипотенузе BD и острым углам ∠DBE, ∠DBM. Из этого следует что, 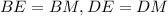 .
.
Также из-за того что, ∠DBC<∠DFC=45°<∠DMC=90°⇒F∈BM, теперь можно пользоваться тем что 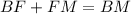 .
.
Заметим что, DFM - прямоугольный треугольник с углом 45°, то есть 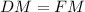 .
.
Учитывая доказанные равенства получаем,
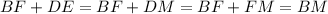
Что требовалось доказать.
площадь АВСД=1/2* АС*ВД*sin СОД, угол АОД=180-уголСАД-уголАДВ=180-30-30=120, уголСОД=180-120=60
площадь АВСД=1/2*8*8*корень3/2 = 16*корень3
средняя линия = площадь/высота = 16*корень3/4=4*корень3