Семья Пушкина - одна из наиболее интересных для изучения тем, ведь род был одним из древних России. Схема родословной, упоминаемой в Государевым родословце, относится к XVI веку. Фамилия происходила от прозвища некоего Григория Пушки. Род имеет дворянский герб.
дворянский герб.
Содержание:
Предки А. С. Пушкина Родители А. С. Пушкина Дети в семье Пушкиных Семья А. С. Пушкина Потомки А. С. Пушкина Интересные факты
Предки А. С. Пушкина
Генеалогическое древо рода Пушкиных венчает имя великого поэта. Но корни уходят в средневековую Русь. В своем стихотворении, которое так и называется “Моя родословная”, А. С. Пушкин упоминает своих предков, служивших Александру Невскому и Ивану Грозному. Самый известный - прадедушка по материнской линии, Абрам Петрович Ганнибал. Биография этого человека была богатой. По происхождению он был арап, родом из Византии. Его подарили императору как некую экзотику. Арап стал любимцем Петра Великого, ему дали имя и отчество. Абрам Петрович служил при дворе: изучал инженерное дело, фортификацию. После смерти императора Ганнибал попал в опалу.1
Николай Петрухин
18 подписчиков
Семья А. С. Пушкина - история и интересные факты родословной
Партнерский материал
10 апреля
1,8 тыс. дочитываний
1,5 мин.
Семья Пушкина - одна из наиболее интересных для изучения тем, ведь род был одним из древних России. Схема родословной, упоминаемой в Государевым родословце, относится к XVI веку. Фамилия происходила от прозвища некоего Григория Пушки. Род имеет дворянский герб.
дворянский герб.
Содержание:
Предки А. С. Пушкина Родители А. С. Пушкина Дети в семье Пушкиных Семья А. С. Пушкина Потомки А. С. Пушкина Интересные факты
Предки А. С. Пушкина
Генеалогическое древо рода Пушкиных венчает имя великого поэта. Но корни уходят в средневековую Русь. В своем стихотворении, которое так и называется “Моя родословная”, А. С. Пушкин упоминает своих предков, служивших Александру Невскому и Ивану Грозному. Самый известный - прадедушка по материнской линии, Абрам Петрович Ганнибал. Биография этого человека была богатой. По происхождению он был арап, родом из Византии. Его подарили императору как некую экзотику. Арап стал любимцем Петра Великого, ему дали имя и отчество. Абрам Петрович служил при дворе: изучал инженерное дело, фортификацию. После смерти императора Ганнибал попал в опалу.
Семья А. С. Пушкина - история и интересные факты родословной
Долгое время Абрам Петрович жил в Прибалтике, где и познакомился со своей второй женой, прабабкой поэта, немкой по происхождению - Христиной-Региной фон Шеберг. Брак был удачным. Со второй женой у прадеда было 11 детей. Третий сын, Осип Абрамович - дед поэта. Он был военным, карьера складывалась удачно. А вот семейная жизнь не удалась. Женился Осип на богатой и родовитой Марии Алексеевне Пушкиной. Но что-то не заладилось, и он уехал в Михайловское, где провернул брачную аферу: женился на Устинье Толстой, объявив свою первую жену умершей. Вскоре обман раскрылся. Последовало наказание - галерные работы на Черноморском флоте. Уйдя в отставку, Осип Абрамович доживал в Михайловском, обустраивая имение. Его первая жена, Мария Алексеевна Ганнибал, посвятила себя дочери Надежде и ее семье, матери поэта.
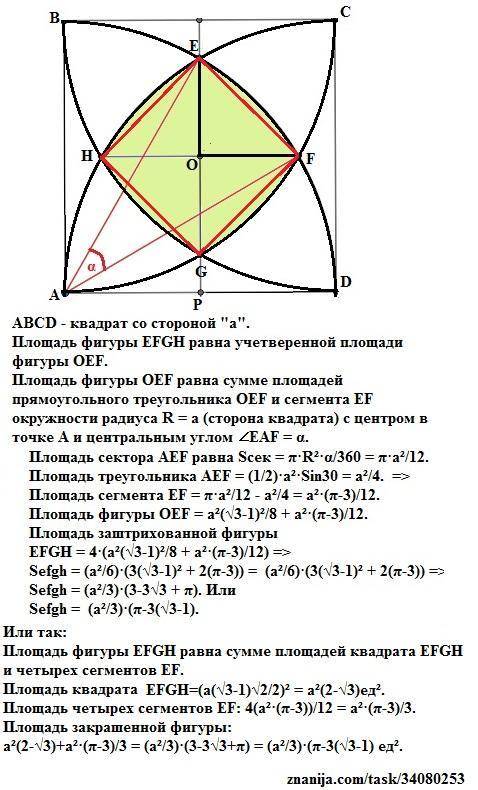
Sefgh = (a²/3)·(π-3(√3-1) ед².
Объяснение:
Пусть АВСD - квадрат со стороной "а".
Площадь фигуры EFGH равна учетверенной площади фигуры OEF.
Площадь фигуры OEF равна сумме площадей прямоугольного треугольника OEF и сегмента EF окружности радиуса R = a (сторона квадрата) с центром в точке А и центральным углом ∠EAF = α.
В треугольнике АЕР по Пифагору: ЕР = √(а²-а²/4) = а√3/2. =>
EO = EP-OP = а√3/2 - a/2 = а(√3-1)/2.
В треугольнике OЕF по Пифагору:
ЕF = √(OE² + OF²) = √(2·(a(√3-1)/2)²) = a(√3-1)√2/2.
Площадь треугольника OEF равна Soef = (1/2)·OE·OF = a²(√3-1)²/8.
По теореме косинусов в треугольнике AEF найдем угол EAF = α.
Cosα = (a² + a² - EF²)/2a² = (2a² - (a(√3-1)√2/2)²)/2a² = 2a²(4 - 3 +2√3 - 1)/(4·2a²) = √3/2.
α = arccos(√3/2) = 30°.
Найдем площадь сегмента EF, отсекаемого от круга (А;R) хордой EF по формуле:
S = Sc - Saef, где Sc - площадь сектора AEF, а Saef - площадь треугольника AEF.
Площадь сектора AEF равна Sсек = π·R²·α/360 = π·а²/12.
Площадь треугольника AEF = (1/2)·а²·Sin30 = а²/4. =>
Площадь сегмента EF = π·а²/12 - а²/4 = а²·(π-3)/12.
Площадь фигуры OEF = a²(√3-1)²/8 + а²·(π-3)/12.
Площадь заштрихованной фигуры
Sefgh = 4·(a²(√3-1)²/8 + а²·(π-3)/12) =>
Sefgh = (a²/6)·(3(√3-1)²+2(π-3))= (a²/6)·(3(√3-1)² + 2(π-3)). =>
Sefgh = (a²/3)·(3-3√3 + π).
Sefgh = (a²/3)·(π-3(√3-1) ед².
Или так:
Площадь фигуры EFGH равна сумме площадей квадрата EFGH и четырех сегментов EF.
Площадь квадрата EFGH= (a(√3-1)√2/2)² = a²(2-√3)ед².
Площадь четырех сегментов EF: 4(а²·(π-3))/12 = а²·(π-3)/3.
Площадь закрашенной фигуры:
a²(2-√3)+а²·(π-3)/3 = (a²/3)·(3-3√3+π) = (a²/3)·(π-3(√3-1) ед².
S=14*12=168