Две прямые, перпендикулярные одной и той же плоскости, параллельны.
PP1 ⊥ ,
QQ1 ⊥ => PP1 II QQ1
Через 2 параллельные прямые можно провести плоскость и притом только одну .
PP1 и QQ1 принадлежат одной плоскости B.
Пусть P1Q1 - линия пересечения плоскостей Альфа и Бета.
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Заданная точка с вершинами исходного треугольника образует наклонные равнобедренные треугольники с боковыми сторонами по 13 см.. Расстояние от этой точки до сторон треугольника в плоскости - это высоты в наклонных треугольниках, которые определяются по формуле: ha = 2√(p(p-a)(p-b)(p-c)) / a Полупериметр для треугольника со сторонами 13, 6, 13 см равен р = (а+в+с) / 2 = (13+6+13) / 2 = 16.см. Расстояние до стороны 6 см равно L = 2√(16(16-13)(16-6)(16-10)) /6 =2√(16*3*6*3) / 6 =2√ 576 / 6 = 2*24 / 6 = 2*√ 1440 / 6 = = 2*37.94733192 / 6 = 12.649111 см. Аналогично до стороны 8 см L = 2√(17(17-13)(17-6)(17-10)) /8 = = 12.369317 см. До стороны 10 см L = 12 см.
PP1Q1Q-квадрат
Периметр равен 41,2 см
Объяснение:
Две прямые, перпендикулярные одной и той же плоскости, параллельны.PP1 ⊥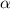 ,
,
QQ1 ⊥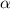 => PP1 II QQ1
=> PP1 II QQ1
Через 2 параллельные прямые можно провести плоскость и притом только одну .PP1 и QQ1 принадлежат одной плоскости B.
Пусть P1Q1 - линия пересечения плоскостей Альфа и Бета.
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.=>PQ II P1Q1
PQQ1P1 - параллелограмм.
Так как < PP1Q1, <QQ1P1 равны 90°, то
PQQ1P1 - прямоугольник.
PP1=PQ => PQQ1P1 - квадрат.
Периметр квадрата находится по формуле:
Р=4а=4×10,3= 41,2 см