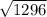 =36
=36A1. Две прямые на плоскости называются параллельными, если они:
4) не пересекаются
А2. Один из признаков параллельности двух прямых гласит:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А3. Выберите утверждение, являющееся аксиомой параллельных прямых:
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной
А4. Если две параллельные прямые пересечены секущей, то:
Соответственные углы равны
А5. Если прямая перпендикулярна одной из двух параллельных прямых, то:
Она перпендикулярна и другой
А6. Всякая теорема состоит из нескольких частей:
Условия и заключения
А7. При пересечении двух прямых секущей образуются углы, имеющие специальные названия:
Накрест лежащие, соответственные, односторонние
А8. Аксиома – это:
Положение геометрии, не требующее доказательства
А9. Выберите утверждение, которое является признаком параллельности прямых:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А10. Если прямая не пересекает одну из двух параллельных прямых, то:
Другую прямую она тоже не пересекает
или
С другой прямой она совпадает
Объяснение:
<B=180°-<A-<C=180°-70°-55°=55°
<B=<C=55°.Против равных углов лежат равные стороны.Значит ΔАВС-равнобедренный с основой СВ.
б)ВМ- является высотой,проведённой к боковой стороне АС.Проведём такой же отрезок с угла С к стороне АВ. Назовём её СР.
ΔАСР=ΔАВМ(АС=АВ,МА=АР,угол А-общий)Значит ВМ=СР,поэтому являются высотами,образующими с соответствующими сторонами прямой угол.Высота делит угол на два:АВМ и МВС.
Из ΔАВМ найдём угол АВМ:
угол АВМ=180°-угол А-угол АМВ=180°-70°-90°=20°
угол МВС=угол В-угол МВА=55°-20°=35°