Объяснение:
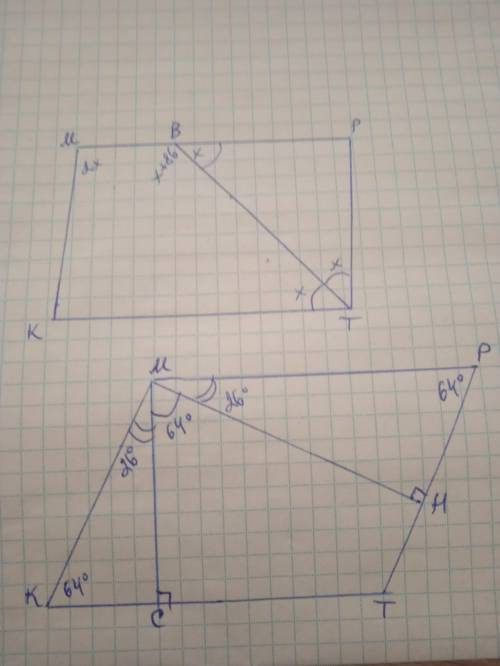
1) Дано: КМРТ - паралелограм, ТВ - бісектриса, ∠МВТ-∠ВТР=86°.
∠К, ∠М, ∠Р, ∠Т - ?
Бісектриса кута паралелограма відсікає від нього рівнобедрений трикутник, отже ΔВРТ - рівнобедрений, ∠РТВ=∠РВТ=х°;
∠РТВ=∠ВТК=х° за визначенням бісектриси
∠МВТ=х+86°
КМВТ - трапеція, сума кутів, прилеглих до бічної сторони трапеції, становить 180°, отже х+х+86=180; 2х=94; х=47.
∠М=∠Т=47*2=94°
∠Р=∠Т=180-94=86°
Відповідь: 86°, 94°, 86°, 94°
2) Дано: КМРТ - паралелограм, МС і МН - висоти, ∠К=∠Р=64°. ∠СМН - ?
ΔКСМ - прямокутний, ∠КМС=90-64=26°
ΔРМН - прямокутний, ∠РМН=90-64=26°
∠К+∠КМР=180°; ∠КМР=180-64=116°
∠СМН=116-26-26=64°
Відповідь: 64°
Відповідь:
Пояснення:
ABCD - паралелограм ; АМ - бісектриса ∠А .
Нехай ∠АМВ = х° , тоді ∠АМС = х + 86° . За власт. суми суміжних
кутів х + х + 86 ° = 180° ;
2х = 180° - 86° ;
2х = 94° ;
х = 47°. BC║AD , AM - січна , тому ∠MAD = ∠AMB = 47° .
∠BAD = 2 * ∠MAD = 2 * 47° = 94° ; тепер ∠В = 180° - 94° = 86° ( за
властивістю кутів пар - ма , прилеглих до однієї сторони ) .
В - дь : 94° , 86° , 94° , 86° .
2) Нехай ВН⊥AD , BF⊥CD , тоді ∠АВН = ∠CBF = 90° - 64° =26° ;
∠HBF = ∠ABF - ∠ABH = 90° - 26° = 64° ; ∠HBF = 64° .
Проекция d меньшей диагонали D пирамиды на основание равна двум радиусам r окружности, вписанной в основание.
d = 2r =2*(a√3/2) = a√3 = √11*√3 = √33 м.
Отсюда находим высоту Н призмы:
Н = √(D² - d²) = √(7² - (√33)²) = √(49 - 33) = √16 = 4 м.
Находим площадь основания:
So = (3√3a²)/2 = (3√3*11)/2 = ((33√3)/2) м².
Теперь можно определить объём призмы:
V = SoH = ((33√3)/2)*4 = (66√3) м³.