ответ:ECG=13,5°
DCF=126°
HCF=54°
Объяснение:так как СЕ биссектриса DCE то она естественно равна половине DCE, тоесть делит угол пополам. Отсюда ECG равно 13,5°. Я думала что я неправильно решила, но здесь чертёж неправильно начерчен, поэтому я скажу как есть. У DCF тоже есть бессектриса, значит она также разделила угол попалам, разделённый угол биссектрисой CE=27°, значит, чьобы узнать скольким градусам равен угол DCF мы должны тупо умножить на два, но я ещё раз говорю чертёж неправильный, объясрите, как тупой угол может быть равен 54°. Отсюда, раз DCH развёрнутый угол и равен 180°, чтобы найти HCF мы просто от 180°-DCF(54°) и вуоля получается 126°. Но так как чертёж неправильный, фиг знает какой там тупой угол. Вооот
Если логично и правильно,то HCF =54,а DCF= 126. Тебе нужно поменять чертёж)
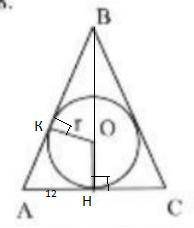
В равнобедренный треугольник АВС , АВ=ВС=15 , АС=24, вписана окружность (О; r). Найдите r.
Объяснение:
1)Пусть ВН ⊥АС. Центр вписанной окружности О лежит в точке пересечения биссектрис. В равнобедренном треугольнике биссектриса совпадает с высотой ⇒поэтому О лежит на высоте ВН.
АН=42 :2=12( т.к. ВН и медиана ) . Будем искать r из ΔКВО.
2) ΔАВН-прямоугольный, по т. Пифагора ВН=√(15²-12²)=9. Тогда отрезок ВО можно выразить так ВО=9-r.
По свойству отрезков касательных АН=АК=12⇒КВ=15-12=3.
3) ΔКВО-прямоугольный , по свойству радиуса , проведенного в точку касания . По т. Пифагора ВО²=ОК²+КВ²
(9-r)²=r²+3² ,81-18r+r²=r²+9 ,18r=72 , r=4 .
Через точку О пересечения диагоналей ромба ABCD проведена прямая OS, перпендикулярная к плоскости ромба, причем OS=6 см, AC=16 см, BD=4√3. Найдите расстояние от точки S до вершин ромба. ( Условие должно быть таким, т.к. АS- расстояние от S до вершины А и С ромба. В условии явно опечатка).
SO перпендикулярен плоскости ромба, значит, перпендикулярен любой прямой, проходящей в плоскости ромба через О.
АО=ВО=16:2=8
ВО=DО=2√3
Из прямоугольных ∆ SOA и ∆ SOD по т.Пифагора
SA=√(SO*+AO*)=√100=10 см
SD=√(AO*+DO*)=√48=4√3 см
SC=SA=10; SD=SB=4√3 см