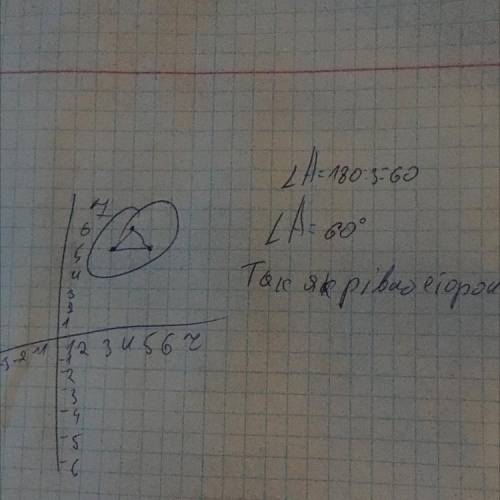
ответ: 8 см²
Объяснение:
КАК решают такие задачи.
Часто подобные задачи решаются вычитания ( или сложения ) площади фигур, образованных клетками. Чертят прямоугольник, который описывает данную фигуру. Вычисляют его площадь, затем площадь "лишних"фигур ( обычно это треугольники) и вычитают. Остается искомая площадь . Или делят данную фигуру на части, у которых удобно найти площадь, и затем складывают.
Обозначим прямоугольник АВСD, опишем около него прямоугольник KLMN. (см. вложение).
S(KLMN)=KL•LM=5•5=25 см²
∆BLC=∆AND по равным катетам.
Их общая площадь Ѕ₁=4•4=16 см²
∆BKA=∆CMD по равным катетам. Их общая площадь
Ѕ₂=1•1=1 см²⇒
Ѕ (ABCD)=S (KLMN)- 16-1=8 см²
----------
Другой
Из ∆ (BLC) по т.Пифагора найдем длину ВС=√(4²+4²)=4√2 см.
Из ∆ (ВКС) по т.Пифагора найдем ширину АВ=√(1²+1²)=√2 см
Площадь прямоугольника равна произведению его длины на ширину:
S(ABCD)=ВС•АВ=4√2•√2=8 см²
ответ:
объяснение:
2. прямую можно обозначать одной маленькой латинской буквой (a,b,
или двумя заглавными латинскими буквами, если этими буквами обозначены точки, расположенные на прямой (ab, cd)
3. у прямой много свойств: через одну точку можно провести бесконечно много прямых, через любые две точки можно провести только одну прямую, у любой прямой, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие
4. прямые, лежащие в одной плоскости и имеющие одну общую точку, которую называют точкой пересечения прямых называют пересекающимися.
6. утверждение, имеющее доказательство, т.е. его надо доказать.
9. их тоже несколько (равные отрезки имеют равные длины, часть отрезка всегда имеет длину, которая меньше длины отрезка, если точки на отрезке делят отрезок на части, то длина отрезка равна сумме длин этих частей.
10. длина отрезка.
11.это точка, которая делит данный отрезок на две равные части.