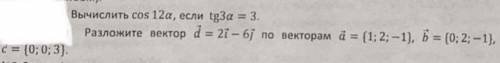
Объяснение:
выразим векторы а, b, c через единичные векторы (орты)
a(1;2;-1) a=i+2j-k
b(0;2;-1) b=2j-k
c(0;0;3) c=3k
1) a-b=i+2j-k-(2j-k)=i
a-b=i
2(a-b)=2i
2)
b=2j-k
3b=3(2j-k)=6j-3k
c=3k
3b+c=6j-3k+3k=6j
3b+c=6j
-(3b+c)=-6j
-3b-c=-6j
3)
2(a-b)=2i
-3b-c=-6j сложим
2(a-b)-3b-c=2i-6j =d
d=2i-6j=2(a-b)-3b-c=2a-2b-3b-c=2a-5b-c
d=2a-5b-c
проверка
a(1;2;-1) a=i+2j-k
b(0;2;-1) b=2j-k
c(0;0;3) c=3k
2a=2(i+2j-k)=2i+4j-2k
-5b=-10j+5k
c=3k
-c=-3k
2a-5b-c=2i+4j-2k-10j+5k-3k=2i-6j=d
примечание
там где буквы надо сверху стрелочки нарисовать что это вектор
Есть два решения этой задачи - стандартное и на сообразительность.
Начну со второго. Учитывая, что расстояние между домами равно сумме высот дома и фонаря, нужного результата мы добьемся, если рассыпем зёрна на расстоянии 6 метров от дома. Тогда катеты левого прямоугольного треугольника равны 8 и 6 метров, правого - 6 и 14-6=8 метров. То есть эти треугольники равны, а тогда у них равны гипотенузы, чего и нужно было добиться.
Первый Если расстояние от первого дома равно x, то квадрат гипотенузы левого треугольника равен 8²+x², а квадрат гипотенузы правого треугольника равен 6²+(14-x)²; а поскольку гипотенузы по условию должны быть равны, получаем уравнение
64+x²=36+196-28x+x²; 28x=168; x=6
Объяснение:
Sбок = 120(2+√3) см².
Объяснение:
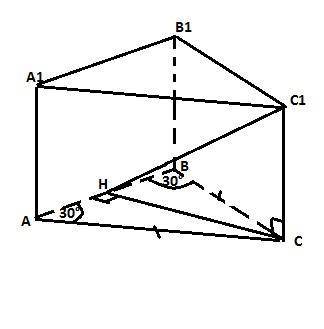
Треугольник АВС равнобедренный (АС=ВС - дано). Его высота - перпендикуляр из вершины С к стороне АВ равен половине боковой стороны, так как лежит против угла 30°.
Итак, СН = 5 см. Расстояние от вершины С1 до стороны АВ - это перпендикуляр С1Н к стороне АВ и его проекция на основание АВС - это высота СН (по теореме о трех перпендикулярах).
Тогда в прямоугольном треугольнике СНС1 катет СС1 по Пифагору равен √(С1Н²-СН²) = √(169-25) = 12 см. Это высота нашей прямой призмы. Тогда площадь ее боковой поверхности равна периметру основания, умноженному на высоту. Учитывая, что сторона АВ равна 10√3 см (из прямоугольного треугольника САН АН = 5√3 см, а
АВ = 2·АН), Sбок = (20+10√3)·12 = 120(2+√3)см²
d(2;-6;0) ; d=k*a+r*b+ p* c;
2=k*1+ r*0+ p* 0 =>k=2 ;
-6= k*2+ r*2+ p*0 , -6=2 *2+2r + p*0, r=-5 ;
0=2*(-1) +(-5) *(-1) + p*3 , p=-1
d=2a -5b- c.