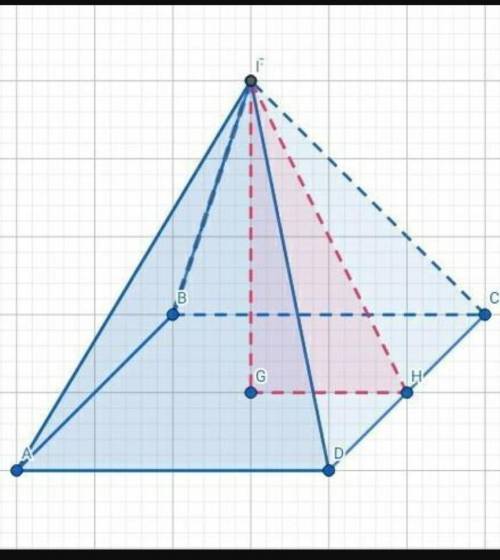
Дано:
Правильная четырёхугольная пирамида .
(см).
(см).
Найти:
(см²).
Значит сначала мы должны найти площадь основания пирамиды, а затем площадь боковой поверхности пирамиды.
В основании правильной четырёхугольной пирамиды лежит квадрат, поэтому (см²).
Площадь боковой поверхности правильной четырёхугольной пирамиды - полупроизведение периметра основания на апофему.
Значит нам нужно сначала найти апофему нашей пирамиды.
1 правило: Апофема делит сторону основания пополам.
2 правило: Катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырехугольной пирамиды.
Объяснение 1 правила: из этого следует, что апофема делит сторону основания так, что (см).
Объяснение 2 правила: внутри нашей пирамиды образовался прямоугольный , где - катет прямоугольного тр-ка (высота пирамиды); - катет прямоугольного тр-ка; - гипотенуза прямоугольного тр-ка (апофема пирамиды). По данному правилу можно сказать, что (см).
Треугольник abd подобен adc.
Объяснение: 1. Угол b равен углу DAC т.к это р/б треугольник и можно найти углы A и C (180-36=144, делим на 2 так как углы равны, равняется 72). AD- биссектриса и делит угл A на 2 (72/2=36, значит BAD и DAC=36)
2. Угол C равен углу BDA так как треугольник BAD - р/б. Так как угл BAD=36 и ABD=36 можно найти BDA (180-36-36=72), а угл C=72 по первому пункту (так как угл A равен углу C как р/б треугольник).
Получается что Угол B=DAC и угол C=BDA
Значит подобны по первому признаку по двум углам
Відповідь:
∠АОС=100°
Пояснення:
ОС=ОВ- як радиус кола, отже ΔОСВ- рівнобедрений з основою СВ. За властивістю рівнобедреного трикутника ∠В=∠С=50°, як кути при основі.
За теоремою про суму трьох кутів трикутника ∠ВОС=180°-(∠В+∠С)=80°.
∠АОВ=180°- як розгорнутий кут
∠АОС= ∠АОВ-∠ВОС=180°-80°=100°