Основанием прямоугольного параллелепипеда является прямоугольник со сторонами 8см и 12см, высота параллелепипеда 15см Найти:а) площадь полной поверхности параллелепипеда. б) объем параллелепипеда. в) площади даигональных сечений

👇

Увидеть ответ

Ответ:

dianaknyazeva

06.12.2021

Sпол=792см²

V=1440см³

S(BB1D1D)=60√13 см²

Объяснение:

а)

Sпол=2(AB*AD+AA1*AD+AB*AA1)=

=2(12*8+12*15+8*15)=2(96+180+120)=

=2*396=792см²

б)

V=AB*AD*AA1=12*8*15=1440 см³

в)

∆АВD- прямоугольный треугольник

По теореме Пифагора

ВD=√(AB²+AD²)=√(8²+12²)=√(64+144)=

=√208=4√13 см

S(BB1D1D)=BD*BB1=4√13*15=60√13 см² площадь диагонального сечения.

Основанием прямоугольного параллелепипеда является прямоугольник со сторонами 8см и 12см, высота пар

4,8(17 оценок)

Открыть все ответы

Ответ:

PraPira

06.12.2021

У нас есть 2 варианта внешнего угла — внешний угол угла, противоположному основанию, и внешний угол угла — противоположный боковой стороне.

Вариант 2-ой таков: угол, противоположный боковой стороне равен: 180-150 = 30°, в этом случае — угол, противоположный основанию равен: 180-(30+30) = 120°.

Боковая сторона равна 10, тоесть нам уже известно 2 стороны равнобедренного треугольника (боковые).

Теперь — зная их, и угол между ними (угол 120 градусов) — найдём основание по теореме Косинусов:

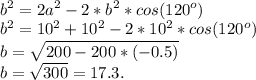
$\displaystyle\\b^2 = 2a^2-2*b^2*cos(120^o)\\b^2 = 10^2+10^2-2*10^2*cos(120^o)\\b = \sqrt{200-200*(-0.5)}\\b = \sqrt{300} = 17.3.$

Нам известны все стороны равнобедренного треугольника.

Формула вычисления радиуса описанной окружности около равнобедренного треугольника такова:

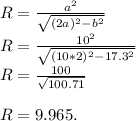
$R = \frac{a^2}{\sqrt{(2a)^2-b^2}}\\R = \frac{10^2}{\sqrt{(10*2)^2-17.3^2}}\\R = \frac{100}{\sqrt{100.71}}\\\\R = 9.965.$

Диаметр в 2 раза больше радиуса, то есть: D = 2R = 19.93.

Вывод: D = 19.93.

Вариант 1-ый:

Внешний угол угла — противоположного основанию, тоесть: α = 180-150 = 30°.

Равные углы, противоположные боковым сторонам равняются: (180-30)/2 = 75°.

На этот раз — формула вычисления основания, зная боковую сторону, и угол между ними — будет такова:

$b^2 = 2a^2-2*b^2*cos(30^o)\\b^2 = 2*10^2-2*10^2* 0.866\\b^2 = 200-173.2\\b = \sqrt{26.8} \Rightarrow b = 5.2.$

В этом случае — радиус описанной окружности равен:

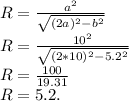
$R = \frac{a^2}{\sqrt{(2a)^2-b^2}}\\R = \frac{10^2}{\sqrt{(2*10)^2-5.2^2}}\\R = \frac{100}{19.31}\\R = 5.2.$

D = 2R = 5.2*2 = 10.4.

Вывод: D = 10.4.

4,4(2 оценок)

Ответ:

Anasstassat

06.12.2021

ответ:Номер 1

Катет является высотой

6•7:2=21 см в квадрате

Номер 2

5•8:2=20 см в квадрате

Номер 3

Проведём высоту,она же в равнобедренном треугольнике является и медианой и биссектрисой.Получились два равных прямоугольных треугольника,где биссектриса 13 см,а один из катетов 5 см(10:2=5).По теореме Пифагора узнаём неизвестный нам катет,он же является высотой.От квадрата гипотенузы вычтем квадрат известного катета

169-25=144

Корень из 144 будет 12

У меня нет значков-корень,квадрат,надеюсь,что ты перепишешь правильно

Высота нам известна-12,узнаём площадь равнобедренного треугольника

10•12:2=60 см в квадрате

Первый ответ Г

Второй ответ. В

Третий ответ Б

Объяснение:

4,7(77 оценок)

Это интересно:

Компьютеры-и-электроника