Раз отрезок д.б. параллелен оси абсцисс, то координаты Y точек M и N должны быть одинаковыми:
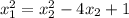
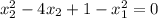
Решим относительно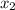 
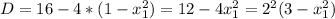
Для того, что бы такие точки существовали, нужно 
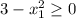
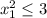
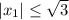
С другой стороны, т.к. длина отрезка MN д.б. равна 3, то:
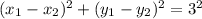
Координаты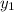 
и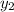 
, как мы уже выяснили равны, т.о.:
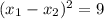
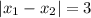
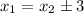
Подставим это в имеющееся уравнение :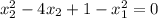
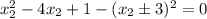
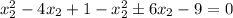
Следовательно: 
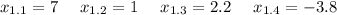
Среди них только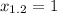 
удовлетворяет условию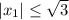
Т.о. координаты точки M(1;1) и точки N(4;1)
Рисунок: http://yotx.ru/default.aspx?clr0=000000&exp0=x%5e2&clr1=666666&exp1=x%5e2-4x%2b1&clr2=ff0000&pv2=on&pt2=%281%3b1%29%284%3b1%29&mix=-10&max=10&asx=on&u=mm&nx=x&aiy=on&asy=on&ny=y&iw=600&ih=400&ict=png&aa=on
Центр описанной вокруг треугольника окружности - точка пересечения срединных перпендикуляров. В правильном треугольнике срединные перпендикуляры - и высоты, и медианы, и биссектрисы.
Медианы треугольника точкой пересечения делятся в отношении 2:1
Радиус вписанной окружности правильного треугольника =1/3 медианы ( высоты)
Радиус описанной окружности правильного треугольника =2/3 медианы ( высоты
Это - вступления для того, чтобы вспомнить, если забыто.
Радиус описанной окружности правильного треугольника=2/3 его медианы.
2/3=10
3/3=15
Медиана =15