
Объяснение:
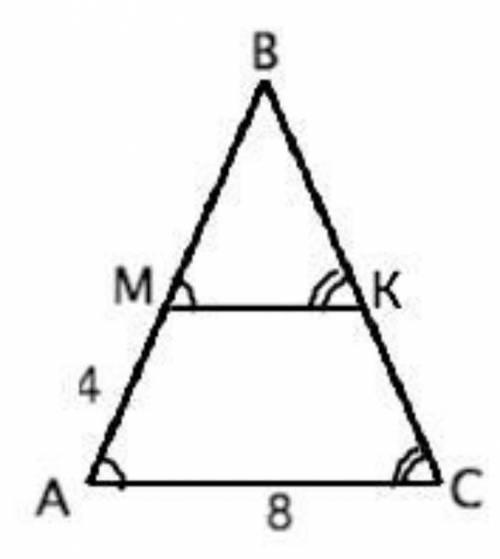
Прямая, параллельная стороне АС треугольника АВС, пересекает его сторону АВ в точке М, а сторону ВС - в точке К. Найдите площадь треугольника АВС, если АМ = 4 см, АС = 8 см, АМ = МК, а площадь треугольника МВК равна 5 см2.
ответ: 20 см²
Объяснение: МК║АС, АВ- секущая, ВС - секущая. Соответственные углы при пересечении параллельных прямых секущей равны, ⇒ ∆ АВС~∆ МВК. По условию МК=АМ=4, АС=8, ⇒ k=AC:МК=8:4=2.
Отношение площадей подобных фигур равно квадрату коэффициента подобия. S(АВС):S(МВК)=k²=2²=4
S(АВС)=S(МВК)•4=5•4=20 см²
При пересечении двух параллельных прямых секущей могут образоваться несколько видов углов:соответсвенные,накрест лежащие и односторонние. Соответственные и накрест лежащие углы друг другу равны,поэтому к данной задаче не подходят,т.к по условию углы разные.Следовательно,данные углы являются односторонними.
Сумма односторонних углов равна 180°.
Дано: <1 и <2-односторонние,<2=5<1
Найти:<1,<2.
<1 +<2=180°
<1 + 5>1=180°
6<1=180°
<1=180°:6
<1= 30°
<2=5•<1=5•30°=150°