Что и требовалось доказать!
Объяснение:
Теорема: "Если при пересечении двух прямых секущей односторонние углы в сумме составляют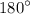 
, то прямые параллельны".
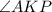и 
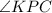- односторонние при пересечении прямых 
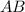и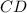 
секущей 
.
.
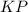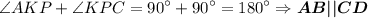Что и требовалось доказать!
- - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Т.к.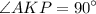 
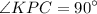
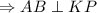и 
и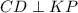 
.
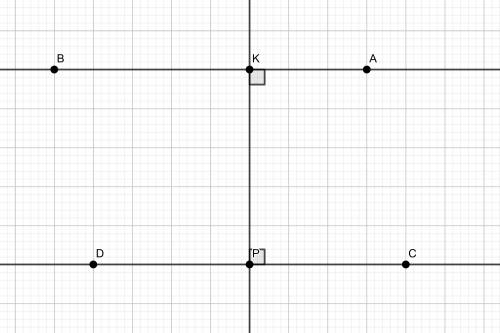
Признак: "Если две различные прямые на плоскости перпендикулярны к одной и той же прямой, то они параллельны".
Т.к. 
и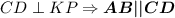 
.
Что и требовалось доказать!
- - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
S=12*3*sin*(1/2)
S=9√3
9√3=12*3*sin*(1/2)
9√3= 36*(1/2)* sin
9√3 = 18*sin
9√3 / 18 = sin
√3/2 = sin
sin 60 = √3/2
ответ: 60