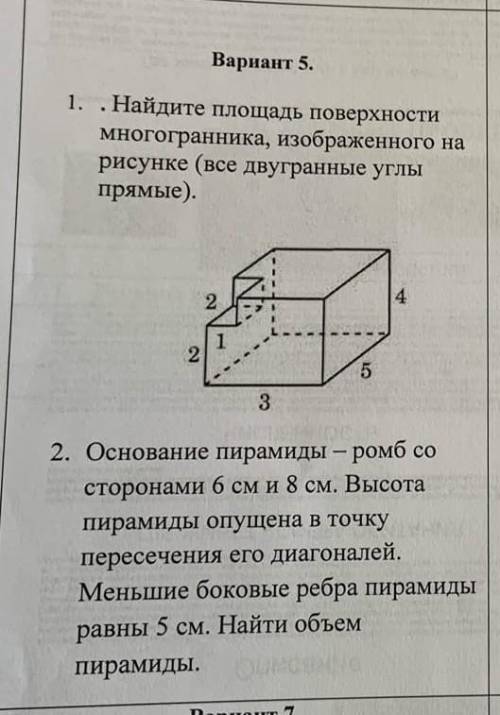
Сумма углов треугольника 180°. Внешний угол треугольника равен сумме двух других, не смежных с ним.
Примем меньший внутренний угол равным х, тогда смежный внешний равен 5х. Их сумма равна градусной величине развернутого угла.
5х+х=180°⇒
х=30°
Случай 1:
Данный равнобедренный треугольник тупоугольный, тогда два его острых угла равны по 30°, третий из суммы углов треугольника равен 180°-2•30°=120°
Случай 2:
треугольник остроугольный. Меньший угол 30°, два других по
(180°-30°):2=75°
1) 30°, 30°, 120°
2) 30°, 75°, 75°
Площадь трапеции S=(a+b)*h/2
60=(a+b)*6/2
(a+b)/2=10 (1)
Треугольники MOC и OCE прямоугольные с общей гипотенузой. Следовательно, они равны между собой
CE=MC=a/2
Треугольники OED и OND прямоугольные с общей гипотенузой. Следовательно, они равны между собой
ED=ND=b/2
CD=CE+ED=a/2+b/2=(a+b)/2=10
Площадь треугольника COD равна 1/2CD*EO=1/2*10*3=15
Треугольник CPD прямоугольный, по т.Пифагора
PD²=CD²-CP²=10²-6²=64
PD=8
С другой стороны
PD=b/2-a/2
b/2=PD+a/2
b/2=8+a/2
b=16+a
Подставляя в (1) найдем a
(a+16+a)=20
2a=20-16
2a=4
a=2
b=16+2=18
Рассматривая прямоугольные треугольники OCE и OED по т.Пифагора находим
OE=√(3²+(a/2)²)=√(9+1)=√10
OD=√(3²+(b/2)³)=√(9+81)=√90=3√10
Cтороны треугольника CPD найдены
Площадь треугольника и его радиус описанной окружности связаны формулой
S=OE·OD·CD/(4R)
R=OE·OD·CD/(4S)
R=√10·3√10·10/(4·15)=300/60=5
ответ: 5 см