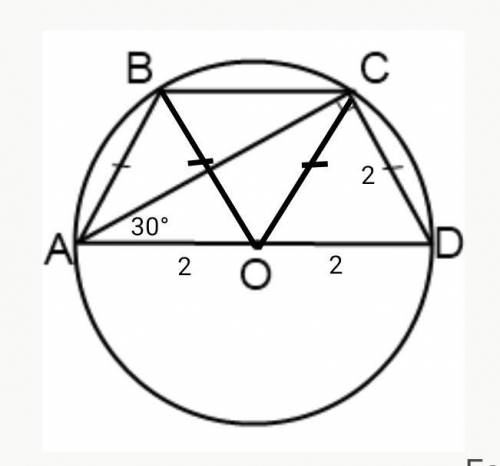
Объяснение:1
1)Сколько общих точек имеют окружность и секущая?
Укажите верные утверждения:
1)3
2)нет общих точек
3)1
4)2 верно
2
Укажите верные утверждения:
1) Вписанный угол измеряется дугой, на которую он опирается верно
2) Окружность и секущая не имеют общих точек
3) Вписанные углы, опирающиеся на полуокружность - прямые верно
4) Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности верно
3
В трапецию, высота которой равна 17, вписана окружность. Найдите радиус этой окружности. R=8,5
4
Градусная мера дуги равна 40 градусов. Найдите градусную меру центрального угла, соответствующего этой дуге 80°
5
Даны окружность с центром О радиуса 5 см и точка А. Через точку А проведены две касательные к окружности. Найдите угол между касательными, если ОА = 10см.
° Отв: 60°
6
Из точки А к окружности с центром О проведена касательная, В - точка касания. Найдите радиус окружности, если АО = 17, АВ = 15. Отв: R=8
7
Сторона квадрата равна 13. Найдите радиус вписанной окружности. Отв: r=6,5
ответ записать без пробелов, единиц измерения, в десятичной дроби ставим ЗАПЯТУЮ!
8
Радиус окружности, проведенный к точке касания...
1)образует с касательной угол меньше 90 градусов неверно
2)образует с касательной угол больше 90 градусов неверно
3)перпендикулярен касательной верно
4)параллелен касательной неверно
9
В равностороннем треугольнике высота равна 15. Найдите радиус описанной окружности Отв: R=10
10
Сколько общих точек имеют окружность и касательная? Отв: 1 общую точку
11
В равностороннем треугольнике радиус вписанной окружности равен 2,7. Найдите радиус окружности описанной около этого треугольника. Отв: R=5,4
12
Градусная мера дуги равна 40 градусов. Найдите вписанный угол, который опирается на эту дугу. Отв: 40°
13
Вписанный угол окружности равен 40 градусов. Найдите градусную меру дуги, на которую он опирается.
Отв: 40°
14
Точки А и В разделили окружность на дуги, градусные меры которых относятся как 4:5. Найдите градусную меру большей дуги. Отв: 200°
15
В ромб вписана окружность.Её радиус равен 13. Найдите высоту ромба. Отв: 26
10 см.
Объяснение:
1. Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. С другой стороны, сумма углов, прилежащих к боковой стороне трапеции, тоже равна 180°, тогда углы при основаниях трапеции равные, и отсюда следует, что вписать в окружность можно только равнобедренную трапецию. В нашем случае трапеция АВСD равнобедренная, АВ = СD = 2 см, ∠CAD = 30°.
2. Так как по условию центр описанной окружности лежит на большем основании, то ∠ АСD вписанный, опирающийся на диаметр, тогда по теореме ∠ АСD = 90°.
3. В прямоугольном треугольнике ACD напротив угла в 30° лежит катет, равный половине гипотенузы, тогда AD = 2•CD = 2•2 = 4 (см).
4. ∆ABO и ∆DCO равные равносторонние, все их углы по 60°, тогда и в равнобедренном ∆BOC ∠BOC = 180° - (60°+60°) = 60°, тогда и он равносторонний, ВС = ОВ = ОС = 2 см
5. Р ABCD = 4 + 2 + 2 + 2 = 10 (см)