DE = 24 см
Объяснение:
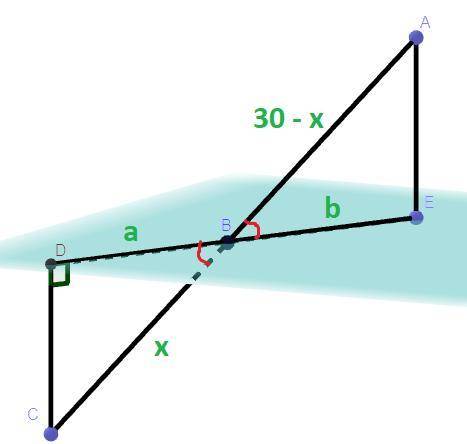
Дано: АС = 30 см, DC = 6 см, AE = 12 см, DC ⊥ ED, AE ⊥ DE
Найти: DE - ?
Решение: Пусть BD = a, BE = b. СB + AB = AC ⇒ AB = AC - BC = 30 - BC.
Пусть BC = x, тогда AB = 30 - x. Треугольник ΔCBD подобен ΔBAE по двум углам так как по условию DC ⊥ ED, AE ⊥ DE, то ∠CDB = ∠AEB = 90°, а углы ∠DBC = ∠ABE как вертикальные углы, из подобия треугольника ΔCBD треугольнику ΔBAE следует, что
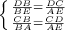
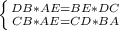
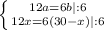
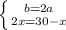
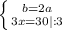
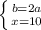
Рассмотрим треугольник ΔCDB. BD = x = 10 см. По теореме Пифагора:
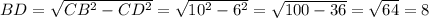 см.
см.
b = 2a ⇔ BE = 2BD = 2 * 8 = 16 см.
DE = BE + BD = 16 + 8 = 24 см.
MD = 2,5 см
Объяснение:
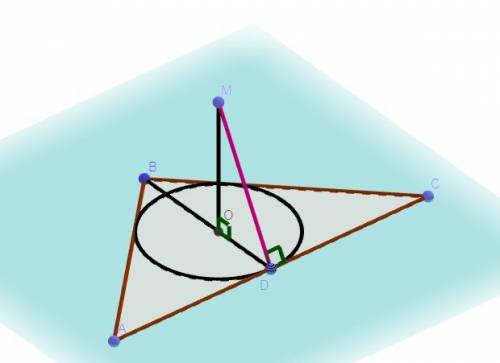
Дано: AC = 6 см, AB = BC = 5 см, О - центр вписаного кола, OM ⊥ ABC,
OM = 2 см, MD ⊥ AC.
Знайти: MD - ?
Розв'язання: За теоремою про три перпендикуляри так як OM ⊥ ABC,
MD ⊥ AC, тоді OD ⊥ AC, отже OD - радіус вписаного кола, так як радіус вписаного кола проведений з центра кола до сторони трикутника і перпендикулярний до сторони. Нехай півпериметр трикутника p, тоді
p = 0,5 * PΔABC = 0,5(AB + BC + AC) = 0,5(5 + 5 + 6) = 0,5 * 16 = 8 см.
За формулами площі триутника слідує наступне:
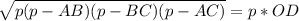
 см.
см.
Розглянемо трикутник ΔMOD. За теоремою Піфагора:
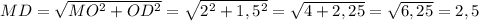 см.
см.
Решение задания прилагаю