трехпроекционном чертеже построить недостающие проекции сквозного отверстия в прямом круговом конусе.
Тема задачи: Вырезы в конусеСоздано:@apriori20 марта 201708:01
Пример текста
мой вариант
мой вариант
пример
пример
Оцените сложность задачи:
0 голосов, средняя сложность: 0.0000
Комментарии
Комментарий
Оставить комментарий
РЕШЕНИЯ ЗАДАЧИ
Создано:@nick20 марта 201710:27
поставьте оценку:
1 голосов, средний бал: 5.0000
Построить недостающие проекции сквозного отверстия в прямом круговом конусе.
рисунок 1
рисунок 1
Комментарии
большое
ответить@apriori20 марта 2017 10:52
Комментарий
ответить@apriori20 марта 2017 14:55
Можете разобраться откуда взялись расстояния?
ответить@apriori20 марта 2017 15:04
ответить@apriori20 марта 2017 16:29
Комментарий
Оставить комментарий
Чтобы предложить решение войдите или зарегистрируйтесь
Записать новую задачу
Все задачи
Все темы
Все инженеры
если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
доказательство:
пусть прямые а и b параллельны и пересечены секущей cd. доказать, что накрест лежащие углы 1 и 2 равны.
предположим, что углы 1 и 2 не равны. тогда от луча cd отложим ∠еcd=∠2 так, чтобы ∠еcd и ∠2 были накрест лежащими углами при пересечении прямых се и b секущей cd.
по построению эти накрест лежащие углы равны, а поэтому прямая cd параллельна прямой b. получили, что через точку с проходят две прямые (а и cе) параллельные прямой b. а это противоречит аксиоме параллельности прямых. следовательно, предположение неверно и угол ∠1=∠2. что и требовалось доказать.
пример.
прямая ав параллельна прямой cd, аd - биссектриса угла bac, а ∠adc=50 градусов. чему равна градусная мера ∠cad?
так как прямые ав и cd параллельны и ad - секущая при этих параллельных прямых, то накрест лежащие углы adc и bad равны. значит, ∠bad=50 градусов.
так как ad - биссектриса ∠bac, то ∠cad=∠bad. следовательно, градусная мера ∠cad=50 градусов.
пример.
прямые ав и cd параллельны. отрезок ав=сd. доказать, что прямая ас параллельна прямой bd.
рассмотрим треугольник abd и треугольник acd.
ав=cd по условию , ad - общая. а углы bad и adc равны как накрест лежащие углы при параллельных прямых ав и cd и секущей аd. следовательно, треугольники abd и acd равны по первому признаку равенства треугольников. а значит, у них соответственные стороны и углы равны.
то есть ∠cad=∠bda. а эти углы являются накрест лежащими при прямых ac и bd и секущей ad. это означает, что прямые ac и bd параллельны. что и требовалось доказать.
пример.
на рисунке ∠cbd=∠adb. доказать, что ∠вса=∠cad.
углы cbd и adb - накрест лежащие углы при прямых ad и bc и секущей bd. а так как эти углы равны, то прямые ad и bc параллельны.
∠вса и ∠cad являются накрест лежащими при параллельных прямых ad и bc и секущей ас, а следовательно, они равны. что и требовалось доказать.
отметим, что если доказана какая-либо теорема, то это не означает, что обратная ей теорема верна.
например, если углы вертикальные, то они равны. а вот если углы равны, то это ещё не означает, что они вертикальные.
1)если две параллельные прямые пересечены секущей, накрест лежащие углы равны.2)если две параллельные прямые пересечены секущей, то соответственные углы равны.3)если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.4)если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
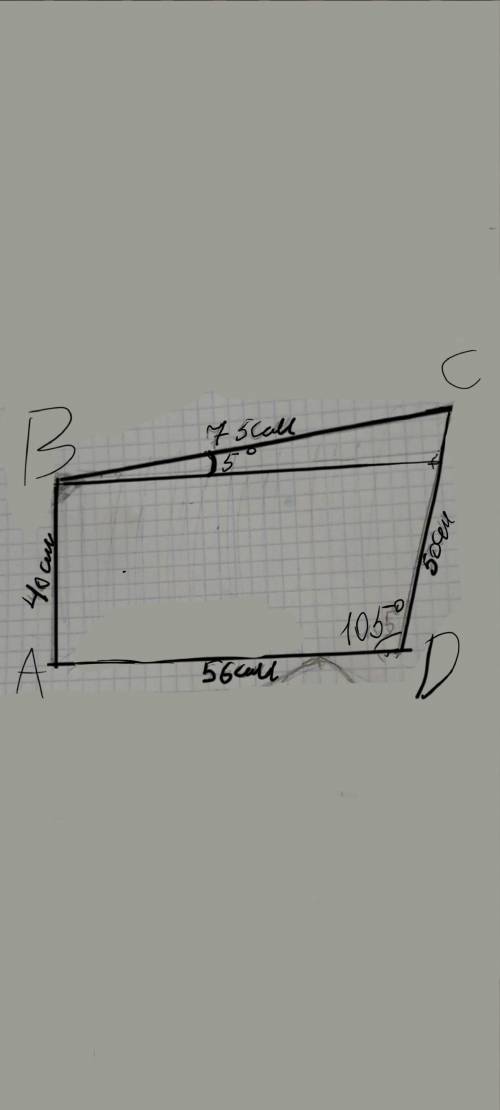
При построении 75 не может быть, там 70. Поэтому исходя из этого решение такое.