1.Тень от фонарного столба будет 4+8=12м, то есть в 12/4=3 раза больше, чем тень от дерева. Значит и высота столба будет в 3 раза больше дерева, то есть 3*3=9м.
2.Треугольник АВС - прямоугольный.
Докажем это с применением теоремы Пифагора:
41²=40²+9²
1681=1600+81
Значит, АС - гипотенуза.
В прямоугольном треугольнике центр окружности находится посередине гипотенузы, следовательно, радиус окружности равен 41:2=20,5 см.
ответ: 20,5 см
3.(картинка)
4.Опустим из вершины равнобедренного треугольника высоту, которая по известной теореме является медианой и биссектрисой. Тогда из получившихся прямоугольных треугольников найдем, что
sin(α/2) = (x/2)/b = x/(2b), где x - это длина искомого основания. Теперь выразим икс.
x = 2b*sin(α/2).
5.Опускаем перпендикуляр BD на сторону AC.
Проекция AB на AC - это AD= AB cos A; проекция BC на AC - это CD= BC cos C.(Картинка 2)Из теоремы синусов
Объяснение:
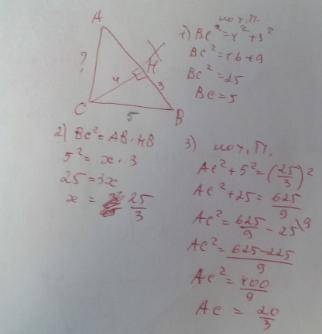
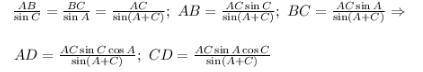
От исходного объема отсекаем 1/2 и 1/8
V(KBQPC) =3/8 V(SABC) =3/8 *1/3 *√3/4 *18^2 *22 =891√3/4
Объяснение:
Правильная треугольная пирамида, в основании равносторонний треугольник.
S(ABC) =√3/4 AB^2 =81√3
V(SABC) =1/3 S(ABC) SH =1/3 *81√3 *22 =594√3
Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.
KQ||AB, QP||BC, KP||AC
△KSP~△ASC (стороны параллельны), KP/AC =KS/AS =1/2
△KQP~△ABC (стороны параллельны), S(KQP)/S(ABC) =(KP/AC)^2 =1/4
△ASH, KH1||AH, т Фалеса: SH1/SH =KS/AS =1/2
V(SKQP) =1/3 S(KQP) SH1 =1/3 *1/4 S(ABC) *1/2 SH =1/8 V(SABC)
Отрезки параллельных прямых между двумя параллельными плоскостями равны.
KH2 =H1H =1/2 SH
V(KABC) =1/3 S(ABC) KH2 =1/3 S(ABC) 1/2 SH =1/2 V(SABC)
V(KBQPC) =V(SABC) -V(KABC) -V(SKQP) =(1 -1/2 -1/8) V(SABC) =3/8 V(SABC) =891√3/4