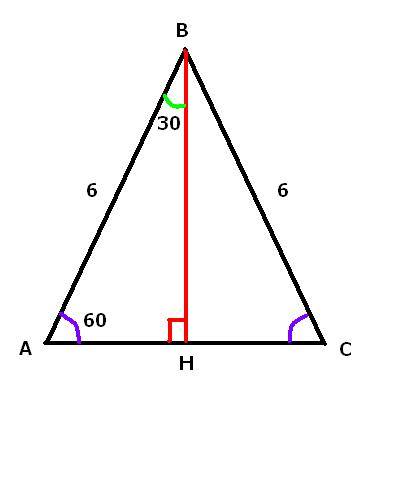
Треугольник АВС - р/б с углом при основании = 60 град. Из вершины треугольника (т.В) проведена высота ВН на основание треугольника АС. Найти высоту ВН, если боковая сторона АВ=ВС=6 см.
Т.к. АВС р/б, то высота проведенная из вершины является и биссектрисой и медианой.
Угол В= 180-60-60=60 см, значит треугольник АВС - равносторонний, тогда угол АВН=СВН=30 град. акже, если АВС - р/с, то АВ=ВС=СА=6см. Тогда, т.к. ВН - медиана, то АН=6/2=3 см. Тогда ВН по т Пиф: ВН=√(6*6-3*3)=√(36-9)=√27=√(9*3)=3√3 см
ответ: ВН=3√3 см.
Рисунок во вложении..................................... ©
ответ: 110°.
Объяснение:
Углы АОМ и МОВ - смежные. Их сумма равна 180°.
Пусть угол АОМ=7х, тогда ВОМ=11х.
Составим уравнение:
7х+11х=180;
18x=180;
x=10.
---------------
Угол АОМ=7х=7*10=70°.
Угол ВОМ=11х=11*10=110°.
-----------------
Угол АОК и уго АОМ - смежные. Их сумма равна 180°. Тогда
АОК=180°-∠АОМ=180°-70°=110°.
Или
Угол АОК и угол ВОМ вертикальные. Поэтому угол АОК равен углу ВОМ:
∠АОК=∠ВОМ=110°.
См. скриншот.