Sboc = 80 ед².
Объяснение:
АА1 и ВВ1 - биссектрисы (дано). Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в этот треугольник (свойство биссектрис треугольника). Следовательно, расстояние от точки О до прямой ВС (являющееся высотой треугольника ВОС), равно радиусу вписанной окружности, равному по условию отрезку ОК (перпендикуляр к стороне АВ) = 8 см.
Тогда площадь треугольника ВОС равна половине произведения высоты на сторону, у которой проведена эта высота. То есть
Sboc = (1/2)·8·20 = 80 ед².
Sboc = 80 ед².
Объяснение:
АА1 и ВВ1 - биссектрисы (дано). Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в этот треугольник (свойство биссектрис треугольника). Следовательно, расстояние от точки О до прямой ВС (являющееся высотой треугольника ВОС), равно радиусу вписанной окружности, равному по условию отрезку ОК (перпендикуляр к стороне АВ) = 8 см.
Тогда площадь треугольника ВОС равна половине произведения высоты на сторону, у которой проведена эта высота. То есть
Sboc = (1/2)·8·20 = 80 ед².
Удачи)))
Объяснение:
ABCDМ - пирамида
AB = BC = CD = AD = 8
AМ = 6 и AМ _|_ ABCD
S осн =
S осн=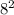
S осн= 64
Δ ABM = ΔAMD,
так как AD=AB и AM - общая →
MB = KD = V(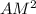
+ 
)
V(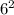
+ 
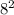) = 10
S (AMB) = S (AMD) = 1\2 * AB * AM = 1\2 * 8 * 6 = 24
S (MBC) = 1\2 * BC * MB = 1\2 * 8 * 10 = 40
S бок = 2*S AMB + S (MBC) = 2*10 + 40 = 60
S полн = S осн + S бок = 64 + 60 = 124