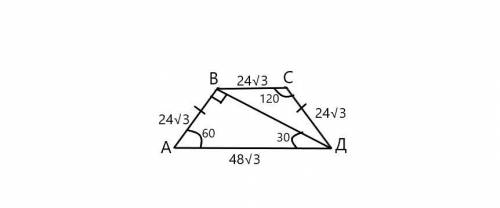
АВ=АД/2 (как катет лежащий против угла 30°) АВ=48√3/2=24√3; СД=АВ (трапеция равнобедренная); углы В и Д в треугольнике ВСД равны 30° (угол В в трапеции (180-60)=120°, угол В в треугольнике (120-90)=30°, угол Д в треугольнике (60-30)=30°); площадь трапеции равна сумме площадей треугольников АВД и ВСД; площадь треугольника равна половине произведения длин сторон на синус угла между ними.
S(АВД)=48√3*24√3*√3/4=864√3;
S(ВСД)=24√3*24√3*√3/4=432√3;
S(АВСД)=864√3+432√3=1296√3 ед².
Можно проще.
S(равнобедренной трапеции)=с*sinα(b-c*cosα), где b - основание , с - боковая сторона, α - угол при большем основании;
S=24√3*√3/2*(48√3-24√3/2)=36*36√3=1296√3 ед².
Еще можно через нахождение высоты, но думаю это лишнее.
2. Каждому многоугольнику можно поставить в соответствие некоторое положительное число (площадь) так, что выполняются следующие условия:
- Равные многоугольники имеют равные площади
- Если многоугольник составлен из двух многоугольников, не имеющих общих внутренних точек, то его площадь равна сумме площадей этих многоугольников.
- Площадь квадрата со стороной, равной единице длины, равна одной единице измерения площади.
Формулы площади треугольника.
1) Площадь треугольника равна половине произведения основания на высоту.
2) Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
3) Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
4) Площадь треугольника равна произведению трех его сторон, деленному на учетверенный радиус описанной окружности.
5) Формула Герона. где р - полупериметр треугольника р=(а+b+c)/2
Формулы площади параллелограмма.
1) Площадь параллелограмма равна произведению основания на высоту.
2) Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.
3) Площадь прямоугольника равна произведению двух его соседних сторон.
4) Площадь ромба равна половине произведения его диагоналей.