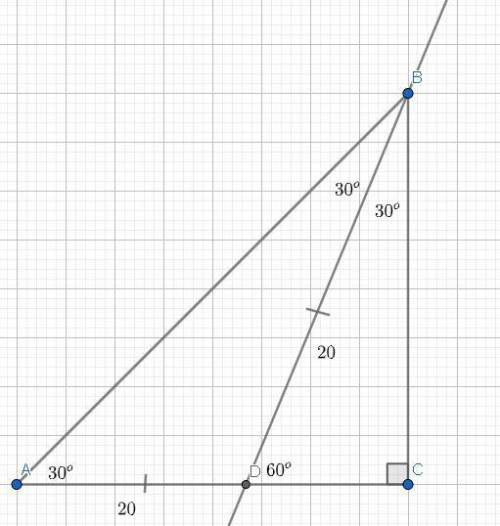
Теорема о 30-градусном угле такова: Катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть катет BC — равен половине гипотенузы AB.
Но нам эта информация не в решении задачи, продолжим.
<B = <C - <A = 90-30 = 60°.
BD биссектриса — делит угол B — пополам, тоесть: <ABC == <DBC = 60/2 = 30°.
<A == <ABD = 30° => AD == DB; треугольник ABD — равнобедренный.
BD = 20 => AD == BD = 20.
<BDC = 30° => DC = DB/2 (теорема о 30-градусном угле прямоугольного треугольника).
DB = 20 => DC = 20/2 = 10
AD = 20; DC = 10 => AC = 10+20 = 30.
Вывод: AC = 30.
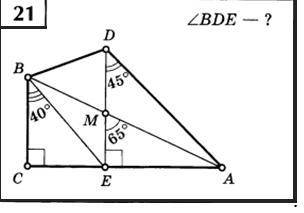
90°
Объяснение:
По свойству трапеции:
Угол С+угол В=180°; угол Д+угол А=180°.
Рассмотрим треугольник ЕДА:
Угол ЕДА=45°; угол ДЕА=90°;
Сумма углов треугольника равна 180°.
Угол ДАЕ=180°-(90°+45°)=45°
Угол ДАС трапеции равны 45°.
Так как по свойству угол Д+угол А=180°, то:
Угол ВДА=180°-45°=135°
Угол ВДА=угол ЕДА+угол ВДЕ. Отсюда следует, что:
Угол ВДЕ=угол ВДА-угол ЕДА; угол ВДЕ=135°-45°=90°