Дано: ABCD — параллелограмм,AF — биссектриса ∠BAD,F ∈ BC.Доказать: ∆ ABF — равнобедренный.Доказательство:1) ∠BAF=∠DAF (так как AF — биссектриса ∠BAD по условию).2) ∠BFA=∠DAF (как внутренние накрест лежащие углы при BC ∥ AD м секущей AF).3) Следовательно, ∠BAF=∠BFA.4) Следовательно, треугольник ABF — равнобедренный
с основанием AF (попризнаку).5) Следовательно, AB=BF.Что и требовалось доказать.Дано: ABCD — параллелограмм,AF — биссектриса ∠BAD,F ∈ BC.Доказать: ∆ ABF — равнобедренный.Доказательство:1) ∠BAF=∠DAF (так как AF — биссектриса ∠BAD по условию).2) ∠BFA=∠DAF (как внутренние накрест лежащие углы при BC ∥ AD м секущей AF).
Средняя линия делит трапецию на две трапеции с равной высотой. Обозначим основания трапеции через а и b, а среднюю линию через с. Проведем в каждой из новых трапеций среднюю линию - d и е. Отношение площадей трапеций S1/S2 = (d*h)/(e*h) = d/е Найдем средние линии трапеций. По условию: а: b = 7:11 отсюда: а = b*7/11 Средняя линия исходной трапеции: с = (а+b)/2 = (b*7/11 + b)/2 = b*9/11 Средние линии полученных трапеций: d = (а+с) /2 = (b*7/11 + b*9/11)/2 = b*8/11 е = (с+b)/2 = (b*9/11 + b)/2 =b*10/11 Отношение площадей: S1/S2 = d/е = (b*8/11)/(b*10/11) = (b*8*11)/(b*10*11) = 8/10 = 4/5 = 4:5 S1 : S2 = 4:5
ответ: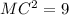
Объяснение:
во вложении