Центр окружности лежит на пересечени высот, которые относятся 2/1 считая от вершины, мы обозначим их как х и 2х, то что 2х это радиус. В раврностороннем треугольнике высота, это медиана и бессиктриса, так что она делит основание на два, соответстаенно пол основания это 6. Теперь по теореме пифагора высота= корень из12 в квадрате- 6 в квадрате, корень из 144- 36, равно корень из 108, но это вся высота а нам надо две части, поэтому:3х=корень из 108, х=корень из 108/3, 2х= 2 корня из 108\3, теперь диаметр в 2 р больше радиуса так что он =4 корня из 108\3.
Объяснение:
3) По теореме Пифагора
АВ²=АС²+СВ²
АВ²=35²+12²
АВ=√(1225+144)=√1369
АВ=37 см
Квадрат катета =произведению гипотенузы на проекцию этого катета
СВ²=АВ*DB
12²=37*DB
DB=144÷37=3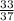
,AD=37-3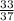=33
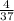
Квадрат высоты = произведению проекций этих катетов
CD²=DB*AD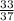=3*33=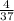
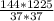, CD=√(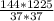)=12*35/37=420/37
8)AB=2+18=20 м
Квадрат высоты = произведению проекций этих катетов
CD²=AD*DB=2*18=36
CD=6 м
Квадрат катета =произведению гипотенузы на проекцию этого катета
AC²=AD*AB, АС=√(2*20)=2√10
По т. Пифагора
АВ²=АС²+АВ², СВ²=АВ²-АС²
СВ²=20²-(2√10)² , СВ=√(400-40)=√360=6√10
ответ: длина отрезка, соединяющего центр нижнего основания с точкой на окружности верхнего основания:
10
Объяснение:
Давайте, обозначим искомый отрезок, скажем, за "х".
Если сделать чертеж (я надеюсь, Вы это сможете сами), то будет очевидным, что отрезки:
радиус , соединяющий центр нижнего основания с точкой на окружности верхнего основания (т.е. искомый отрезок "х")составляют прямоугольный треугольник. (Так как цилиндр, по умолчанию "прямой, круговой" и образующая перпендикулярна основанию.) При этом отрезок "х" будет гипотенузой, ведь он лежит против прямого угла.
По теореме Пифагора:
R² + L² = x² (где R - радиус основания, L - образующая) ⇒
⇒ x = √(R² + L²) = √(6² + 8²) = √(36 + 64) = √(100) = 10
Следовательно, х = 10