УДАЧИ)
Объяснение:
S бок=1/2·Р осн·SK
S K=5см
Р осн=2·S бок/SK
P осн= 2·80/5
P осн =32 см
Р осн=4·АВ.
АВ=Р осн/4
AB=32/4
AB=8см.
ОК=1/2·АА
OK=1/2·8
OK=4 см.
SOK- прямоугольный треугольник
За т. Пифагора
SO=√(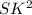 -
-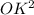 )
)
SO=√(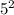 -
-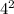 )
)
SO=3см
S осн=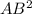
S осн=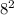
S осн=64 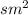
V=1/3*Sосн*SO=1/3*64*3=64 см³
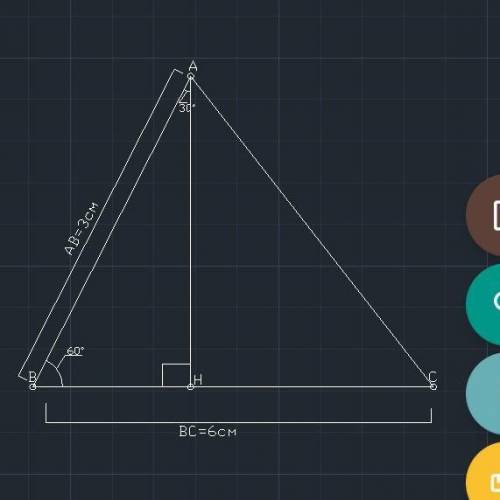
а) Опустим высоту АН из вершины угла, и рассмотрим получившийся прямоугольный треугольник АВН,
{< - угол}
<Н=90°, по определению прямоугольного треугольника, зная сумму всех углов этого треугольника, найдем <ВАН
<ВАН=90°-60°=30°
Против угла в 30° лежит катет равный половине гипотенузы, а значит ВН=0,5*3=1,5
Найдем АН по теореме Пифагора
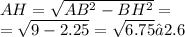
Найдем НС, зная ВН и ВС,

Рассмотрим треугольник АСН, прямоугольный,
Отсюда,
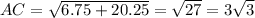
б) Периметр треугольника равен сумме сторон,
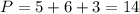
в)Площадь треугольника равна половине произведения АВ на НС и на SinB
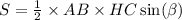
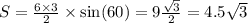
или
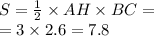
г) Радиус окружности можно вывести из формулы
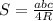
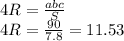

ΔОСВ равносторонний. В нем углы при вершинах С и В равны.т.к. ОС=ОВ= радиусы одной окружности. Т.е. равнобедренный получается. но поскольку углы С и В еще и по 60°в, то и угол О в этом треугольнике 60 °. Тогда внешний угол АОВ равен сумме двух внутренних ∠ В и ∠С, с ним не смежными, т.е. он равен 60°+60°=120°, а тогда в равнобедренном треуг. АОВ ∠ А =∠ В= 30 °,
(180°-120°)/2=30°, как углы при основании равнобедренного ΔАОВ, т.к. АО и ВО радиусы одной окружности и ∠DАС = 90°, т.к. радиус, проведенный в точку касания перпендикулярен касательной АD, значит, искомый ∠ DАВ =90°-30°=60°
ответ 60 °
Объяснение:
V=64 см³
Объяснение:
Sбок=1/2*Росн*SK
SK=5см высота грани.
Росн=2*Sбок/SK=2*80/5=32 см
Росн=4*АВ.
АВ=Росн/4=32/4=8см.
ОК=1/2*АА=1/2*8=4 см.
∆SOK- прямоугольный треугольник
По теореме Пифагора
SO=√(SK²-OK²)=√(5²-4²)=3см
Sосн=АВ²=8²=64 см²
V=1/3*Sосн*SO=1/3*64*3=64 см³