Відповідь:
15 см. 20 см. 25 см.
Пояснення:
Квадрат высоты проведенной к гипотенузе равен произведению величин отрезков на которые он делит гипотенузу.
H^2 = 9 × 16 = 144
Теперь рассмотрим два треугольника, полученные при делении высотой исходного на два. Они оба прямоугольные, одним катетом является высота H, а вторыми катетами являются отрезки по 9см. и 16см.
Катеты исходного треугольника равны:
sqrt ( 144 + 81 ) = sqrt ( 225 ) = 15 см.
sqrt ( 144 + 256 ) = sqrt ( 400 ) = 20 см.
Гипотенуза равна:
9 + 16 = 25 см.
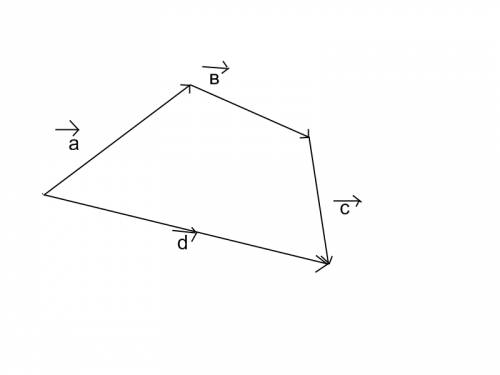
три сложения векторов: правило треугольника( складываютя 2 вектора, больше- многоугольника) : суммой двух векторов наз вектор соединяющий начало первого вектора с концом последнего, при условии что конец одного вектора находится в начале следующего;
правило параллелограмма: Суммой двух векторов исходящих из одной точки, называется вектор , исходящий из той же точки и являющийся диагональю параллелограмма АВСD, построенного на этих же векторах рис 2
сложение векторов a-> b-> c-> на первом рисунке
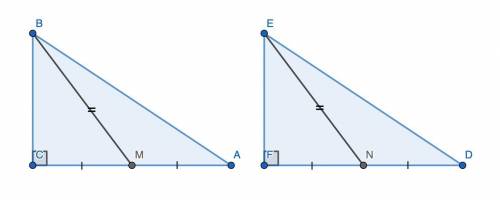
Рассмотрим прямоугольные треугольники ABC и DEF с прямыми углами C и F, у которых AC = DF, M и N — середины AC и DF соответственно, BM = EN.
Поскольку AC = DF, CM = AC / 2, FN = DF / 2, то CM = FN. Рассмотрим треугольники BCM и EFN. Они прямоугольные, CM = FN по доказанному, BM = EN по условию. Тогда треугольники BCM и EFN равны по катету и гипотенузе, а значит, BC = EF.
Рассмотрим треугольники ABC и DEF. Они прямоугольные, AC = DF по условию, BC = EF по доказанному. Значит, они равны по двум катетам, что и требовалось доказать.
АС=20см
СВ=15см
АВ=25см
Объяснение:
АВ=АК+КВ=9+16=25см
АС=√(АВ*АК)=√(16*25)=4*5=20см
СВ=√(АВ*КВ)=√(25*9)=5*3=15см