
Пусть АВСД четырёхугольник, вписанный в окружность,
<A : < B : < C = 2 : 6 : 7. Примем часть за х. То есть
<A = 2 * х; < B = 6 * х; < C = 7 * х.
Как известно в четырёхугольнике, вписанном в окружность сумма противоположных углов равна 180°, то есть <A + < C = 180°, <B + <Д = 180°.
<A + < C = 2 * х + 7 * х = 9 * х = 180°. х = 180°/9 = 20°.
<A = 2 * х = 2 * 20° = 40°;
< B = 6 * х = 6 * 20° = 120°;
< C = 7 * х = 7 * 20° = 140°;
< Д = 180° - < В = 180° - 120° = 60°.
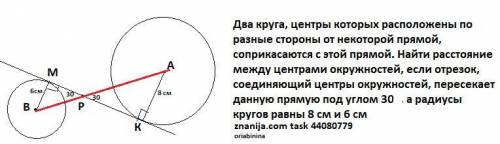
Два круга, центры которых расположены по разные стороны от некоторой прямой, соприкасаются с этой прямой. Найти расстояние между центрами окружностей, если отрезок, соединяющий центры окружностей, пересекает данную прямую под углом 30°, а радиусы кругов равны 8 см и 6 см
Объяснение:
Введем обозначения , как показано на чертеже. Расстояние между центрами это отрезок АВ. Он равен АР+ВР
1) ΔАКР-прямоугольный по свойству касательной и радиуса , проведенного в точку касания . Угол ∠АРК=30° , значит гипотенуза АР=2*8=16 (см).
2) ΔВМР-прямоугольный по свойству касательной и радиуса , проведенного в точку касания . Угол ∠ВРМ=30° , значит гипотенуза ВР=2*6=12 (см).
3) АВ=16+12=28(см) .
====================
Свойство " Радиус , проведенный в точку касания , перпендикулярен касательной.
ответ: 72см²
Объяснение: полупериметр параллелограмма равен: 44/2=22см
Примем АВ за 5 частей, а АD за 6 частей.
Сумма частей равна 5+6=11 и это составляет 22 см
Одна часть будет равна: 22/11=2см
АВ=2*5=10см
АD=2*6=12см
АH=АВ*cosА=10*(3/5)=6см
BH=√АВ²-АH²=√10²-6²=√100-36=√64=8cм
HD=AD-AH=12-6=6см
S(HBCD)=(HD+BC)/2*BH=(6+12)/2*8=9*8=72см²