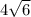;KM=5. (ответ:12,5)
1) 3 см
2) ≈ 28°
3) ≈ 37°
4) 144 см²
Объяснение:
Пирамида правильная, значит основание - квадрат, боковые грани - равные равнобедренные треугольники, высота проецируется в центр основания - точку пересечения диагоналей квадрата.
SO - высота пирамиды.
∠SAO - угол наклона бокового ребра к плоскости основания (так как АО - проекция ребра SA на плоскость основания)
Пусть Н - середина CD, тогда SH - медиана и высота равнобедренного треугольника SCD, т.е. апофема пирамиды.
∠SHO - угол наклона боковой грани к плоскости основания (так как SH⊥CD и ОН⊥CD по теореме, обратной теореме о трех перпендикулярах)
1) SH = 5 см
OН = AD/2 = 4 см как средняя линия треугольника ACD.
ΔSOH: (∠SOH = 90°), по теореме Пифагора
SO = √(SH² - OH²) = √(5² - 4²) = 3 см
sin∠SHO = SO/SH = 3/5 = 0,6
3) ∠SHO = arcsin 0,6 ≈ 37°
2) AC = AB√2 как диагональ квадрата,
АС = 8√2 см, АО = АС/2 = 4√2 см
ΔSAO: (∠SOA = 90°),
tg∠SAO = SO/AO = 3 / (4√2) = 3√2/8
∠SAO = arctg 3√2/8 ≈ 28°
4) Sполн = Sосн + Sбок
Sосн = АВ² = 8² = 64 см²
Sбок = 1/2 Pосн · SH = 1/2 · 4 · 8 · 5 = 80 см²
Sполн = 64 + 80 = 144 см²
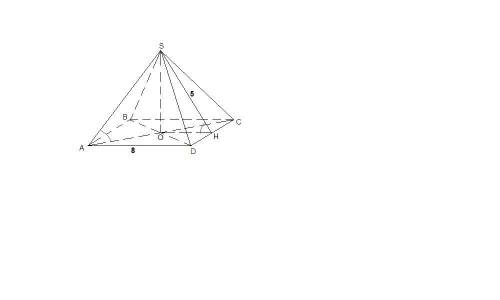
Искомая площадь - сумма площадей двух сегментов круга, отсекаемых от него ромбом.
Угол СТО опирается на диаметр и равен 90º
Расстояние от точки до прямой - длина отрезка из этой точки, перпендикулярного к этой прямой.
ОТ ⊥ ВС и является расстоянием от О до ВС.
ТО=3 см ( расстояние от точки до прямой - перпендикуляр)
Формула площади сегмента ромба:
S=0,5R²[(πα/180º)-sin α],
где R радиус круга, α - угол сегмента в градусах, π≈3,14
∆ ВОС~∆ ВОТ ( прямоугольные с общим углом при В)
∠ВОТ=∠ВСО
tg∠ВОТ=ВТ:ТО=√3:3=1/√3. Это тангенс 30º
∆ ТО1С равнобедренный.
∠ ТСО₁=∠ СТО₁
∠ ТО₁С=180-2∠ТСО₁
Отсюда ∠ТО₁С=180º-2*30º=120º
Из ∆ ТОС
ОС=ТО:sin30º=3:0,5=6 см
R=ОС:2=3 см
Сумма площадей 2-х сегментов
S=R²[(πα/180º)-sin α],
sin 120º=√3/2
Подставим найденные величины:
S=3²[(π120º/180º)-√3/2]
S=6π-9√3)/2
S=6π-4,5√3≈11,055 см²
-------
В приложении решение дано несколько иное, хотя принцип тот же.
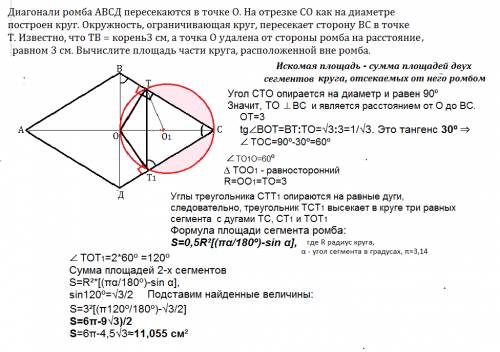
AB²=AC²+BC²
AB²=4²+(4√3)²
AB²=16+16*3
AB²=64
AB=8