Объяснение:1. Две прямые называются параллельными, если они
г) не пересекаются на плоскости
2. Две прямые параллельны, если при пересечении их секущей
г) внутренние накрест лежащие углы равны
3.Две прямые параллельны, если при пересечении их секущей
в) сумма внутренних односторонних углов равна 180 градусов;
4.Две прямые параллельны, если при пересечении их секущей
а) соответственные углы равны;
5)Сколько параллельных прямых можно провести через точку не лежащую на данной прямой
б) одну;
6)Две прямые пересечены секущей. Чему равна сумма внутренних односторонних углов, если внутренние накрест лежащие углы равны?
а) 180°
7) Две прямые пересечены секущей. Внутренние односторонние углы в сумме составляют 180 градусов, а один из соответственных углов равен 36 градусов. Чему равен второй из соответственных углов?
г)36°
8). Сумма внутренних накрест лежащих углов при параллельных прямых и секущей равна 220^0. Чему равны эти углы?
в)110°
9). Один из внутренних односторонних углов при параллельных прямых и секущей равен 50 градусов. Найдите второй внутренний односторонний угол. Отв: 180°-50°=130°; Отв: 130°
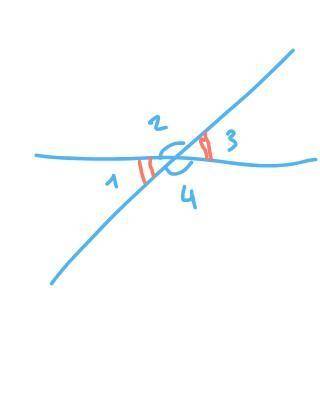
При пересечении двух прямых образуются четыре угла.
Вертикальные углы — у которых стороны одного угла являются продолжениями сторон другого угла. Вертикальные углы равны. Есть две пары вертикальных углов — ∠1 и ∠3, ∠2 и ∠4.
Смежные углы — два угла, у которых одна сторона общая, а две другие дополняют друг друга до прямой. Смежные углы в сумме равны 180°. Есть четыре пары смежных углов — ∠1 и ∠2, ∠2 и ∠3, ∠3 и ∠4, ∠1 и ∠4.
По условию, сумма трёх углов равна 196°.
∠1 + ∠2 + ∠3 = 196°.
∠1 и ∠2 — смежные углы, ∠1 + ∠2 = 180°, => ∠3 = 196° – 180° = 16°.
∠1 и ∠3 — вертикальные углы, ∠1 = ∠3 = 16°, => ∠2 = 196° – 16° – 16° = 164°.
Итого, ∠1 = ∠3 = 16°, ∠2 = ∠4 = 164°.
Меньший угол — ∠1 и ∠3 — равен 16°.
ответ: 16°.
Дано: коло (О; r), АВ - хорда, OM + MN = r, АВ перпендикулярна до ON, OM = 9 см, MN = 6 см.
Знайти: АВ.
Розв'язання
За властивістю хорди, радіус, перпендикулярний хорді, ділить хорду навпіл. Отже, АМ = МВ. Оскільки ОА і ОВ - радіуси, то ОА = ОВ = 9 + 6 = 15 (см).
∆ОАМ = ∆ОВМ, оскільки ОА = ОВ, АМ = ВМ, а кут ОМА = кут ОМВ = 90°.
Із ∆АОМ за теоремою Піфагора: АМ = √(АО^2 - ОМ^2). АМ = √(225 - 81) = √144 = 12 (см).
АМ = МВ, отже АВ = 12 + 12 = 24 (см).
Відповідь: 24 см.