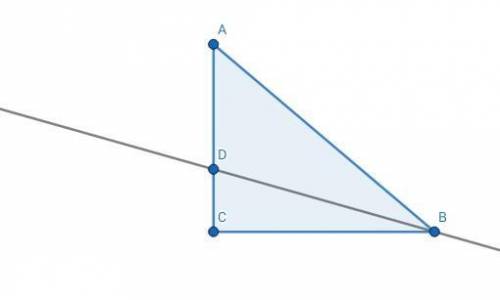
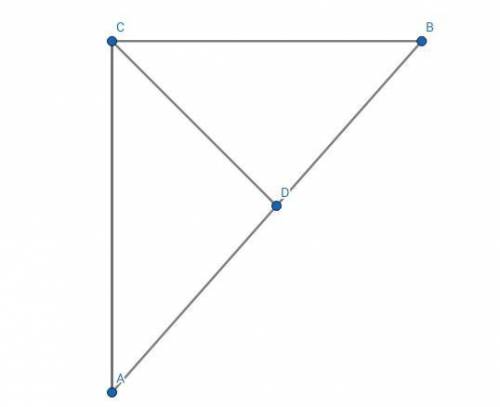
Сумма смежных углов равна 180°.
∠ADB смежный с ∠BDC => ∠BDC = 180° - 110° = 70°
Сумма углов треугольника равна 180°.
=> ∠DBC = 180° - (90° + 70°) = 20°
Так как BD - биссектриса => ∠DBC = ∠DBA = 20°
∠DBC = ∠DBA = 20°=> ∠ABC = 20 × 2 = 40°
Сумма углов треугольника равна 180°.
=> ∠BAD = 180° - (90° + 40°) = 50°
ответ: 50°.
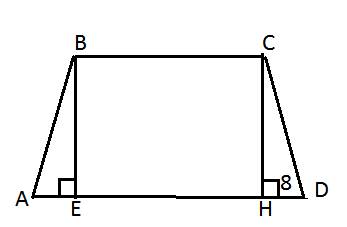
Задача#2.Сумма острых углов прямоугольного треугольника равна 90°.
=> ∠А = 90° - 45° = 45°
Так как ∠А = ∠В = 45° => ∆АВС - равнобедренный.
=> CD - высота, медиана, биссектриса.
Медиана, проведённая из прямого угла к гипотенузе, равна половине гипотенузы.
=> АВ = 8 × 2 = 16 см.
ответ: 16 см
См. Объяснение
Объяснение:
Стандартные размеры винтовой лестницы (если позволяет место, где эта лестница монтируется):
1) Наружный диаметр = ширина лестничного марша (без учёта диаметра внутреннего столба) х 2 =
60 · 2 = 120 см - минимум;
95 · 2 = 190 см - максимум.
2) Внутренний диаметр (диаметр столба) - 15 см;
3) Стандартный шаг винта, или высота подъёма на 1 оборот = 2,2 м.
4) Высота подступенка (шаг между одноименными точками ступеней) - 20 см (шаг включает толщину ступени; если ступени из дерева, то их высота должна быть порядка 5 см, или ≈2 дюйма); чем меньше высота подступенка, тем легче подниматься по лестнице.
РАСЧЕТ
1) Угол поворота.
За 1 полный оборот мы поднимемся вверх на 2,2 м. Останется подняться ещё на:
3 - 2,2 = 0,8 м.
Пересчитаем 0,8 м высоты в градусы поворота:
0,8 : 2,2 · 360 = 131°
Значит, при подъёме на 3 м мы повернём в итоге на:
360 + 131 = 491°- то есть точка выхода с лестницы будет не над точкой входа, а за ней - на расстоянии чуть больше 1/3 окружности.
2) Количество ступеней:
3000 мм (высота подъёма) : 200 мм (высота подступенка) = 15 ступеней.