1) находим высоту пирамиды 6*sin60=6*sqrt(3)/2=3*sqrt(3)
Находим площадь основания
S=3R^2sqrt(3)/4
R=6*cos60=3
S=3*9sqrt(3)/4=27sqrt(3)/4
V=1/3hS=27*sqrt(3)*3sqrt(3)/3*4=81/4=20,25
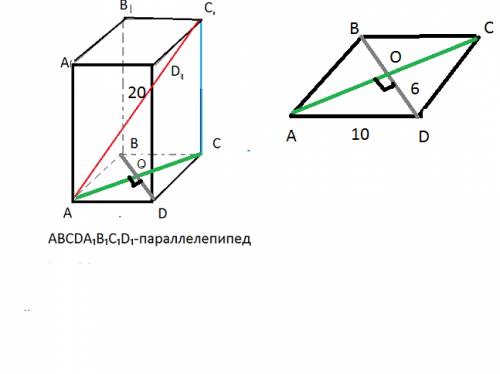
2) Пусть ВС=2а, угол АВС=30 градусам. Тогда 2a/AB=cos30 Отсюда находим АВ=4а/sqrt(3), тогда радиус окружности R=2a/sqrt(3) Заодно находим АС=2a/sqrt(3) Перейдем к нахождению высоты. Искомая грань SCB Проведем ОЕ перпендикулярно ВС (одновременно ОЕ параллельна АС и является средней линией и потому равна половине АС, ОЕ=a/sqrt(3)). По теореме о трех перпендику лярах SE тоже будет перпендикулярна ВС и потому линейный угол двугранного угла равен SEO=45/ Тогда SO=OE Высота найдена.Далее находим объем конуса по стандартной формуле.
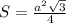
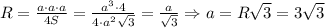
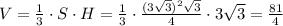 куб. см
куб. см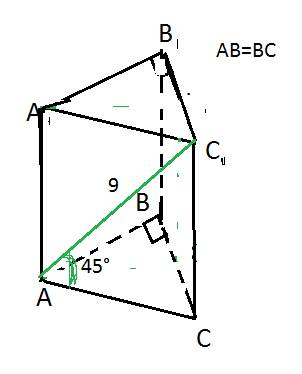
ответ: 1 ) 30° ; 2 ) 60° .
Объяснение:
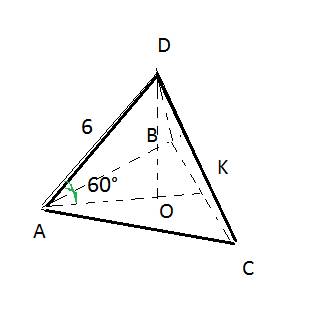
ΔАВС - правильний ; DA ⊥(ABC) ; AD = AB ;
1 ) ∠( AB , ( ADE) ) = ∠BAE = 1/2∠CAB = 1/2 * 60° = 30° ;
2 ) ∠( AC , ( ABD) ) = ∠CAB = 60° .