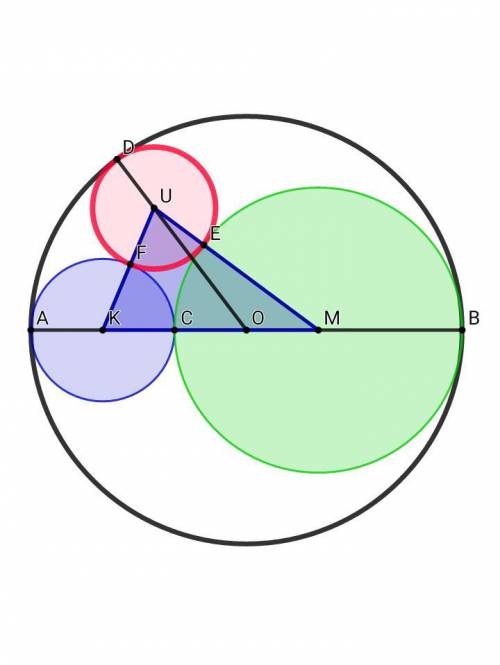
Пусть радиус красной окружности R = x, тогда КМ = KC + CM = 21 + 42 = 63, KU = FU + KF = x + 21, MU = UE + ME = x + 42, UO = DO - DU = 63 - x
Применим теорему косинусов для ΔКМU:
KU² = KM² + UM² - 2•KM•UM•cos∠KMU
(x + 21)² = 63² + (x + 42)² - 2•63•(x + 42)•cos∠KMU
x² + 42x + 441 = 3969 + x² + 84x + 1764 - 126•(x + 42)•cos∠KMU
126•(x + 42)•cos∠KMU = 42x + 5292 ⇒ cos∠KMU = (x+126)/3(x+42)
Теперь ещё раз применим теорему косинусов уже для ΔUOM:
UO² = OM² + UM² - 2•OM•UM•cos∠OMU
(63 - x)² = 21² + (x + 42)² - 2•21•(x + 42)•cos∠OMU
x² - 126x + 3969 = 441 + x² + 84x + 1764 - 42•(x + 42)•cos∠OMU
42•(x + 42) = 210x - 1764 ⇒ cos∠OMU = (5x - 42)/(x + 42)
cos∠KMU = cos∠OMU ⇒ (x + 126)/3(x + 42) = (5x - 42)/(x + 42)
x + 126 = 3•(5x - 42) ⇔ 14x = 252 ⇔ R = x = 18 ⇒ D = 36
ответ: 36
ответ: S б = 18 кв. од .
Объяснение:
Нехай ΔАМВ - бічна грань тіраміди і АМ = L , ∠AMB = 120° ;
MN ⊥AB , MN - апофема . ∠AMN = 1/2 *120° = 60° , тому ∠MAN = 30° .
Звідси MN = 1/2 AM = 1/2 L . Із прямок. ΔAMN AN = √ ( AM² - MN²) =
= √ [ L² - ( L/2 )²] = L√3/2 ; AN = L√3/2 ; AB = 2* AN = L√3 ; AB = L√3 .
S б = 1/2 P ос * MN ; S б = 1/2 * 3 *L√3 * 1/2 L = 3√3 L/4 . Із ΔАМВ
за теоремою синусів AB/sin120° = 2R ; R = AB/2sin120° = L√3/(2√3/2) = L .
За умовою R = 8√3 , тому L = R = 8√3 . Тепер вже обчислимо S б :
S б = 3√3 L/4 = 3√3 * 8√3/4 = 18 ( кв. од .) .