Рисунок приложен. По признаку параллелограмма сумма соседних углов равна 180 градусов.
То есть ∠C + ∠D = 180°
∠ECD + ∠ EDC = 
∠C + ∠D = (∠C + ∠D) = * 180° = 90°
Из этого следует, что в ΔECD ∠CED = 180 - 90 = 90°.
∠GEM = ∠CED = 90° как вертикальные углы
Аналогично ∠GFM = 90°.
Если у паралелограмма (а это паралелограмм из правила:
Биссектрисы противоположных углов параллелограмма параллельны или лежат на одной прямой,
следовательно, противоположные стороны четырехугольника паралельны,а это параллелограмм
Или же
∠BNA = ∠NBC как накрест лежащие углы при BC ║AD и секущей BN
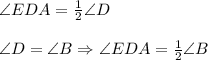
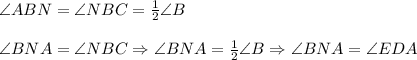
∠BNA = ∠EDA, AD - секущая ⇒ BN ║DJ
Аналогично AO||CP
Из этого следует, что FGEM - параллелограмм
) хоть один угол 90°, то это прямоугольник.
Доказано
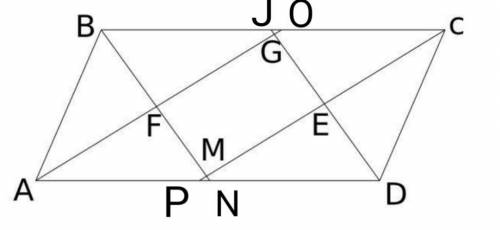
1. ΔABC-правильный . R и r-радиусы вписанной и описанной окружностей. Выразите R через r.
a₃ = 2r√3 и a₃ = R√3 ⇒ 2r√3= R√3 , R=2r.
4. Найдите площадь равностороннего треугольника, вокруг которого описано окружность радиуса 3 см.
a₃ = R√3 ⇒ a₃ = 3√3 см
S(равностороннего треуг.)=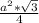 
⇒ S(равн.треуг.)= 
= 
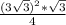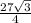(cм²)
5. Определите количество сторон правильного многоугольника углы которого равны 160 градусов.
Многоугольник правильный , поэтому сумма всех внутренних углов 160*n .
160*n=180(n-2) , 160n=180n-360 , 20n=360 , n=18. Количество сторон 18.
((n-2)/n*180- формула для нахождения углов в правильном многоугольнике )
6. В правильный треугольник ,сторона которого 4√3 cм, вписана окружность. Вокруг окружности описан квадрат. Найдите сторону квадрата.
a₃ = 2r√3 , 4√3= 2r√3 ⇒ r=2 см.
Квадрат описан около окружности, значит сторона квадрата равна
a₄ =2r или a₄ =4см.
Объяснение:
Решение на фото