Очка B принадлежит отрезку AС. Через точку A проведена плоскость α. Через точки B и С проведены параллельные прямые, пересекающие плоскость α в точках B1 и С1 соответственно. а) Докажите, что точки A, B1 и С1 лежат на одной прямой

б) Найдите CB, если CС1 = 12 см, BB1 = 4 см, AB = 5 см

👇

Увидеть ответ

Ответ:

elitael

27.07.2020

б) тр. АСС1 подобен тр. АВВ1 по двум углам (уг. А - общий; уг. ВВ1А =уг. СС1А тк ВВ1 || СС1)

составим пропорцию

12/4=(х+5)/5;

х+5=12×5/4=15

х=10

ВС=10см

Объяснение:

а) не знаю как написать, так что извиняй)

4,5(67 оценок)

Открыть все ответы

Ответ:

nata506

27.07.2020

Объяснение:

1)Если <С=90°, то АС и ВС - катеты, а АВ- гипотенуза. Косинус угла - это отношение прилежащего к углу катета к гипотенузе, используем эту формулу для нахождения гипотенузы АВ:

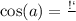
$\cos(a) = \frac{АС}{АВ} \\$

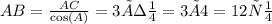
$AB= \frac{AC}{ \cos(A) } =3÷ \frac{1}{4} = 3×4=12см$

Теперь найдём ВС по теореме Пифагора:

ВС²=АВ²–АС²=12²–3²=144–9=135; ВС=√135=3√15см

ответ: АВ=12см, ВС=3√15см

2) синус - это отношение противолежащего от угла катета к гипотенузе поэтому

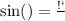
$\sin(А) = \frac{ВС}{АВ}$

тогда АВ=

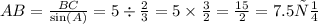
$AB = \frac{BC}{ \sin(A) } = 5 \div \frac{2}{3} = 5 \times \frac{3}{2} = \frac{15}{2} = 7.5см$

теперь найдём АС по теореме Пифагора:

АС²=АВ²–ВС²=7,5²–5²=56,25–25=31,25; АС=√31,25=

=2,5√5см

ответ: АВ=7,5см, АС=2,5√5см

3) тангенс - это отношение противолежащего от угла катета к прилежащему:

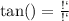
$\tan(В) = \frac{АС}{ВС}$

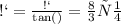
$ВС = \frac{АС}{ \tan(В) } = \frac{8}{3} см$

Теперь найдём АВ по теореме Пифагора:

АВ²=АС²+ВС²=

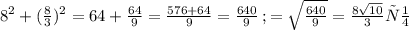
$8 {}^{2} +( \frac{8}{3} ) {}^{2} = 64 + \frac{64}{9} = \frac{576 + 64}{9} = \frac{640}{9} \:; АВ = \sqrt{ \frac{640}{9} } = \frac{ 8\sqrt{1 0 } }{3} см$

ответ: АВ=8√10/3см, ВС=8/3см

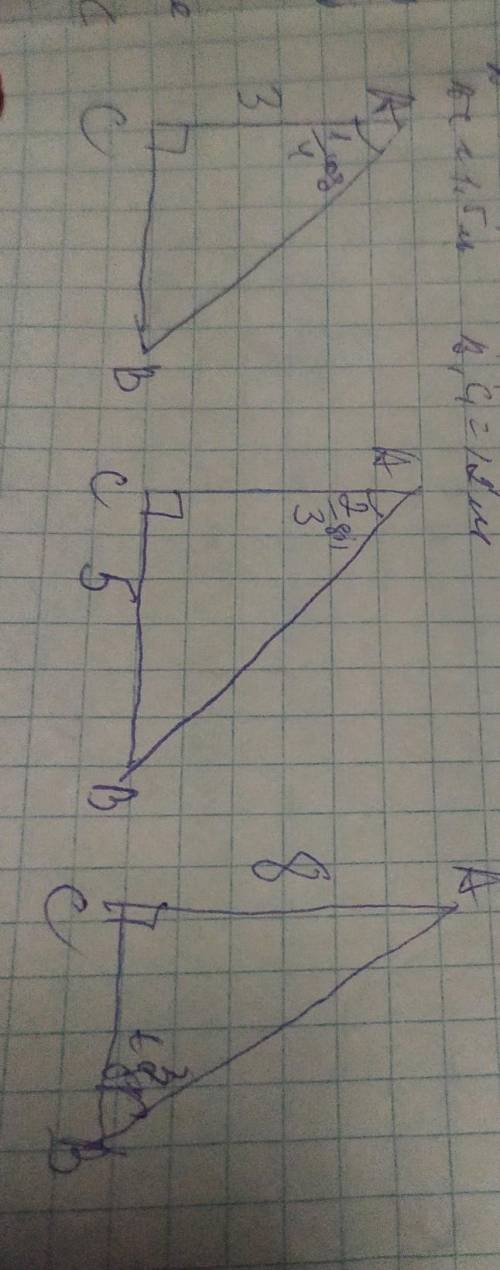
Найдите неизвестные стороны прямоугольного треугольника ABC (Угол C =90°), если: 1) AC = 3 см, cos A

4,4(48 оценок)

Ответ:

Cherep666

27.07.2020

Расстояние от точки P до плоскости правильного шестиугольника со стороной 8 см равно 8 см. Найдите расстояние от точки P до сторон шестиугольника, если она равноудалена от каждой из них.

• Если точка Р равноудалена от сторон правильного шестиугольника, то она проецируется в центр шестиугольника, то есть в точку пересечения его бо'льших диагоналей, в точку О.

• Опустим из точки О перпендикуляр ОТ к СD. РО перпендикулярен ОТ, ОТ перпендикулярен CD, следовательно по теореме о трёх перпендикулярах РТ перпендикулярен CD, то есть PT - искомое расстояние.

• Бо'льшие диагонали правильного шестиугольника делят его на шесть правильных, то есть равносторонних треугольников.

• В тр. COD: OT = CDV3 / 2 = 8V3 / 2 = 4V3 см

В тр. РТО : по т. Пифагора РТ = V( ( 4V3 )^2 + 8^2 ) = V( 48 + 64 ) = V112 = 4V7 см.

ОТВЕТ: 4V7.

4,6(14 оценок)

Это интересно:

Взаимоотношения

19.03.2022

Как прийти в себя после разрыва отношений...

Кулинария-и-гостеприимство

05.10.2021

Как правильно жарить курицу: секреты и рекомендации...