Эта точка S называется вторая точка Брокара. Почему вторая? Если считать углы при вершине против часовой стрелки, то у первой точки равные углы идут первыми, а у второй - вторыми, как в этой задаче.
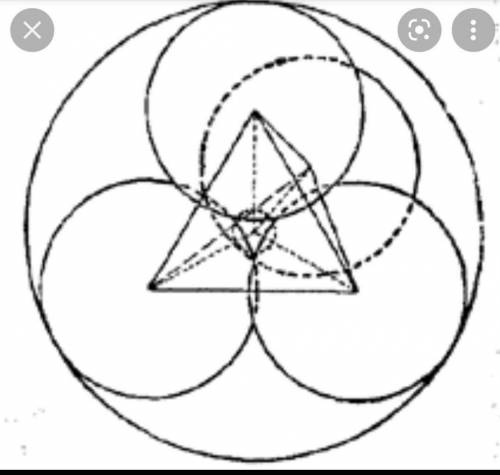
См. чертеж. Я изобразил известное построение точки Брокара. Окружности касаются сторон в одной из вершин. Окружность с центром G касается KL в точке L, окружность с центром в точке Q касается MK в точке K. Окружность (заданная в задаче) с центром O касается ML в точке M, но так как треугольник равнобедренный, то эта окружность заодно касается и KL в точке K.
∠MKS - вписанный в окружность (O) (я буду для краткости так именовать окружности - центр в скобках) и опирается на дугу MS; эта дуга лежит между касательной ML и хордой MS => ∠MKS = ∠SML;
Точно также с использованием окружности (G) и её дуги LS легко показать что ∠SML = ∠KLS; то есть равенство углов, заданное в условии, корректно соблюдается, плюс обнаружен и третий равный угол
∠MKS = ∠SML = ∠KLS (именно это равенство углов и есть определение точки Брокара, а номер определяется порядком углов)
Кроме того, в условии задано ∠SKL=60°, и как теперь ясно, также и ∠SMK = ∠LMK - ∠SML = ∠LKM - ∠MKS = ∠SKL = 60°; величина угла пока не нужна (она понадобится позже), а вот равенство ∠SMK = ∠SKL уже необходимо, поскольку △MKS и △KLS подобны по 2 углам (это подобие - следствие того, что △MKL равнобедренный).
Так как KL - общая внешняя касательная окружностей (G) и (O) (это еще одно следствие того, что треугольник равнобедренный), а прямая MS - радикальная ось этих окружностей, точка их пересечения P лежит посредине KL (обратите внимание - это "соль" всего решения!)
LP = PK;
(Из этого факта следует целый фейерверк следствий, что называется, следите за руками :))
△MKS и △KLS подобны, и отрезки SN и SP - медианы из соответствующих вершин этих треугольников. Поэтому SN/SP = MS/SK;
Отрезок SK - одновременно меньшая сторона в △KLS и "средняя" в △MKS, в данном случае это пропорция между соответствующими элементами разных треугольников. Однако эта пропорция означает, что стороны △MKS и △NSP пропорциональны.
∠LSP = ∠KSN (это опять углы между соответствующими сторонами и медианами подобных треугольников, но можно и сказать, что △LSP и △KSN подобны); => ∠NSP = ∠MSK; => △NSP подобен △MSK;
но это еще не все :) оба эти треугольника подобны △KLS, но, как средняя линия, PN = ML/2 = KL/2; а значит, SP = SL/2; SN = SK/2;
Есть еще много интересных следствий, например, PSNK - вписанный четырехугольник, и еще много интересного, но для решения достаточно именно этого результата, SN = SK/2;
Теперь есть все, чтобы найти ∠MKS = x; вот теперь понадобится что ∠SMK=60°; так как величины углов не зависят от реальных размеров, можно взят подобный треугольник, у которого SK = 2, SN = 1; и я обозначу MS = 2a; MK = 2b; я не стал рисовать NT II MS; NT = a; T - середина SK.
Прекрасное геометрическое решение этой задачи дано в я всем советую сейчас "сбегать туда", сам же я просто сосчитаю угол по теореме косинусов.
из △TNK (со сторнами TK = 1; NK = b; NT = a; по сути я принял TK за единицу измерения длины)
1 = a^2 + b^2 - ab; (напомню, что ∠SMK = 60° = ∠TNK;)
a^2 = b^2 + 1 - 2b*cos(x);
из △SNK 1 = 4 + b^2 - 4b*cos(x);
Дальше исключается cos(x); 4b*cos(x) = b^2 + 3;
2a^2 = 2b^2 + 2 - 4b*cos(x) = 2b^2 + 2 - (b^2 + 3) = b^2 - 1; b^2 = 2a^2 + 1;
a^2 + 2a^2 + 1 - a√(2a^2 + 1) = 1; 3a = √(2a^2 +1); 7a^2 = 1; a = 1/√7;
b^2 = 2/7 + 1 = 9/7; b= 3/√7; cos(x) = (b^2 + 3)/(4b) = 5/√28; sin(x) = √(3/28);
Так как расстояние от S до MK равно √2 = SK*sin(x); а расстояние от S до KL пусть это H = SK*sin(60°) = √2*sin(60°)/sin(x) = √14;
Я публикую еще один решения.
После того, как все слова про равные углы сказаны (см. начало решения), можно сразу записать уравнение с теоремы Чевы в тригонометрической форме.
(sin(y)/sin(x))*(sin(60°)/sin(x))*(sin(60°)/sin(x)) = 1; y =∠SLM;
Все углы "отсчитываются" против часовой стрелки у каждой вершины.
(y + x) + (60° + x) + (60° + x) = 180°; => y = 60° - 3x;
sin(60°-3x) = (4/3)*(sin(x))^3; вот это уравнение надо решить. Ну что, тут только раскрывать все и искать уравнение, которое можно решить.
(√3/2)cos(3x) = (1/2)sin(3x) + (4/3)(sin(x))^3;
(√3)cos(x)(1 - 4(sin(x))^2) = sin(x)(3 - (4/3)(sin(x))^2);
(3√3)ctg(x) = (9 - 4(sin(x))^2)/(1 - 4(sin(x))^2) =
= (9(1 + (ctg(x))^2) - 4)/(1 + (ctg(x))^2 - 3) = (5 + 9(ctg(x))^2)/((ctg(x))^2 - 3);
теперь, чтобы избавиться от иррациональности, можно ввести новую переменную z = (√3)ctg(x); ctg(x) = z/√3; тогда
3z = (5 + 9z^2/3)/(z^2/3 - 3) = (15 + 9z^2)/(z^2 - 9);
или z^3 - 3z^2 - 9z - 5 = 0; получилось кубическое уравнение. Внимательный читатель наверняка заметит, что у уравнения есть корень (-1), что позволяет понизить степень до квадратного, но я сделаю вид, что этого не вижу (как и корня 5), и просто попытаюсь выделить полный куб.
z^3 + 3z^2+3z + 1 - 6z^2 - 12z - 6 = 0;
(z + 1)^3 - 6(z + 1)^2 = 0; или (z - 5)(z + 1)^2 = 0; корень (-1) "не физический",
То есть ctg(x) = 5/√3; sin (x) = √(3/28); получился тот же результат.

"Кенгуру" . Большой треугольник разделили на маленькие треугольники как показано на рисунке. В середине каждого треугольника записан его периметр в метрах. Чему равен периметр большого треугольника?
Решение
Введем обозначения , как показано на рисунке.
Одну из сторону треугольника с периметром 15 разобьем на два отрезка с длинами z1 ,z2.
Частички сторон большого треугольника прономеруем. Тогда
Р ( большого треуг)= 1 + 2+ 3+ 4+ 5+ 6+ 7+ 8=
=(1+2) + 3+ (4+5) + 6 + (7+8)=
=(10-х) +(9-а-z1)+(20-в) +(12-с-z2)+(11-у)=группируем=
=62-(х+у+z1+z2)-(а+в+с)=62-15-13=34.