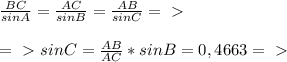
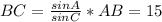
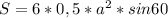 , где а - сторона шестиугольника и любого из правильных треугольников. Зная площадь шестиугольника, мы находим, что
, где а - сторона шестиугольника и любого из правильных треугольников. Зная площадь шестиугольника, мы находим, что 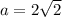 . Каждая сторона шестиугольника стягивает дугу в 360\6= 60 градусов. А каждая сторона квадрата стягивает 360\4=90 градусов. Составим отношение: 60\а=90\б, где б - сторона квадрата. Выразим б. б=90а\60=
. Каждая сторона шестиугольника стягивает дугу в 360\6= 60 градусов. А каждая сторона квадрата стягивает 360\4=90 градусов. Составим отношение: 60\а=90\б, где б - сторона квадрата. Выразим б. б=90а\60=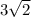 . Площадь квадрата - это квадрат его стороны, поэтому его площадь будет равна 18.
. Площадь квадрата - это квадрат его стороны, поэтому его площадь будет равна 18.
АВ=4√5 см; ВС=2√5 см; S ΔАВС=20 см²
Объяснение:
Дано: ΔАВС - прямоугольный, ∠В=90°;
ВН - высота; АН=8 см; НС=2 см.
Найти: АВ; ВС; S ΔАВС.
Рассмотрим ΔАВС.
-метрические соотношения в прямоугольном треугольнике.