Углы у равнобедренной трапеции одинаковы по 45°.
Проведем из вершины трапеции две высоты на большее основание.
Расстояние между основаниями равно меньшему основанию трапеции, то есть 25 см.
Большее основание по условию 41 см.
41-25=16 см
16:2=8 см - Сторона прямоугольного треугольника, образованного при проведении высоты.
В этом треугольнике угол 45°. значит и второй угол прямоугольного треугольника 45°. (180°-90°-45°= 45°).
Так как углы при основаниях треугольника равны, то треугольник равнобедренный.
Высота совпадает с боковой стороной и равняется тоже 8 см.
ответ: высота трапеции 8 см
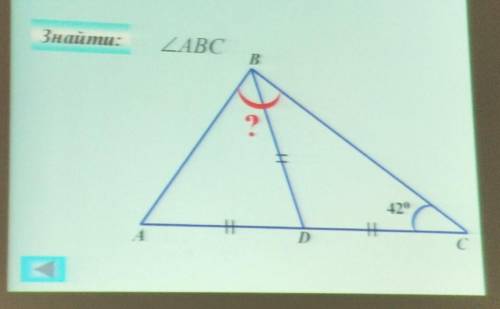
90°
Объяснение:
Угол DBC = 42° (как угол при равнобедренном треугольнике CBD)
угол BDC будет = 180° - (42°+42°) = 96°
Значит угол ADB = 180° - 96° = 84° (смежные углы)
Треугольник ABD тоже равнобедренный
значит угол DAB = ABD = (180°-84°):2 = 48° (как углы при основании равнобедренного треугольника)
Искомый угол состоит из двух углов, просто складываем их величины:
Угол ABC = ABD + DBC = 48°+ 42° = 90°