Объём шара определён формулой: 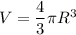 .
.
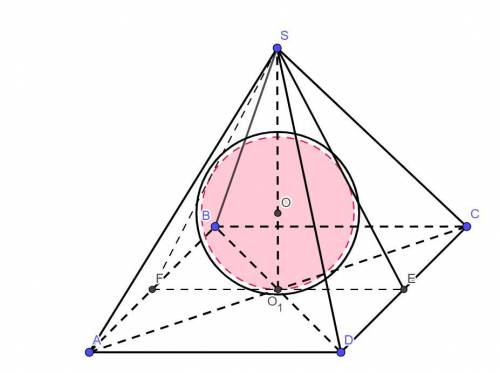
Шар можно вписать в любую правильную пирамиду. Центр шара лежит на высоте пирамиды и совпадает с центром окружности, вписанной в равнобедренный треугольник, боковой стороной которого является апофема пирамиды, а высотой - высота пирамиды. Радиус шара равен радиусу этой окружности.
Радиус шара R, высота пирамиды H и радиус окружности r, вписанной в основание пирамиды, связаны соотношением: 
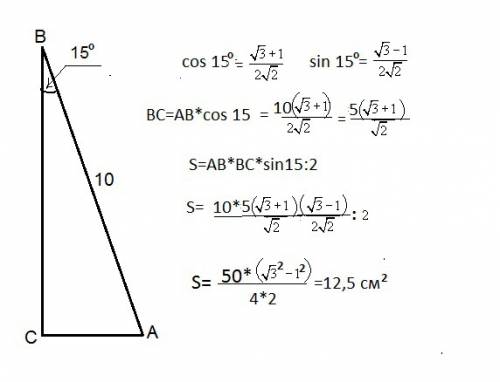
Радиус основания r = AD/2 = 10/2 = 5. Высота пирамиды H определим по теореме Пифагора из треугольника SO₁E, предварительно вычислив апофему SE
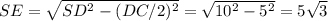
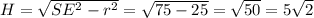
Из заданного соотношения найдём радиус шара
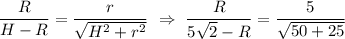
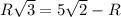
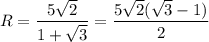
Объём шара: 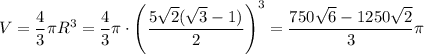
Объяснение:
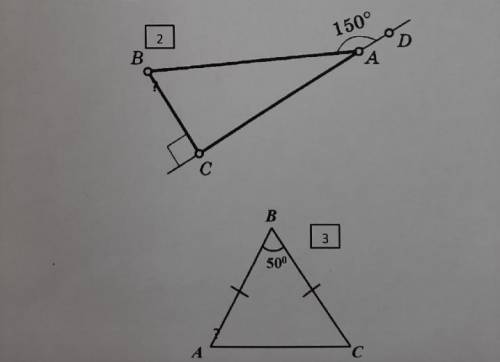
2)
<ВCD=90°; ВС- перпендикуляр
<CAD=180°, развернутый угол
<ВАС=<CAD-<BAD=180°-150°=30°
Сумма острых углов в прямоугольном треугольнике равна 90°
<СВА+<ВАС=90°
<СВА=90°-<ВАС=90°-30°=60°
ответ: <ВСА=90°; <СВА=60°; <ВАС=30°
3)
∆ВАС- равнобедренный треугольник
ВА=ВС, по условию
В равнобедренном треугольнике углы при основании равны.
<А=<С.
Сумма углов в треугольнике равна 180°
<А=(180°-<В)/2=(180°-50°)/2=65°
<С=65°
ответ: <А=65°; <В=65°