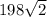На ребре А1D1 необходимо отметить точку Р так чтобы она делила ребро в отношении 3:4 начиная от вершины А1 (Рисунок во вложении). Тогда площадью сечения будет равнобедренная трапеция APQC с основаниями AС и PQ. Найдем основания:
Так как точка Q делит D1C1 в отношении 3:4, начиная от вершины С1 и D1C1=28, то C1Q=12 а QD1=16. Аналогично D1P=16. Найдем PQ
[
Из прямоугольного треугольника CC1Q найдем CQ
В трапеции опустим высоту QH и найдем ее из прямоугольного треугольника QHD. HD это проекция боковой стороны на большее основание и равно полуразности оснований
Площадь трапеции равно произведению полусуммы оснований на высоту
Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции. Свойства средней линии трапеции: Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство: К и М - середины боковых сторон трапеции ABCD, КМ - ее средняя линия.
Проведем прямую ВМ. ВМ ∩ AD = N.
CM = MD по условию, ∠BCМ = ∠NDM как накрест лежащие при пересечении параллельных AN и ВС секущей CD, ∠BMC = ∠NMD как вертикальные, ⇒ ΔBMC = ΔNMD по стороне и двум прилежащим к ней углам.
Значит, ВМ = MN, то есть КМ - средняя линия треугольника ABN, следовательно КМ║AN, а значит и КМ║AD.
Из равенства треугольников следует, что DN = BC = b, значит AN = AD + BC = a + b, а KM = AN/2 = (a + b)/2 как средняя линия треугольника ABN.
На ребре А1D1 необходимо отметить точку Р так чтобы она делила ребро в отношении 3:4 начиная от вершины А1 (Рисунок во вложении). Тогда площадью сечения будет равнобедренная трапеция APQC с основаниями AС и PQ. Найдем основания:
Так как точка Q делит D1C1 в отношении 3:4, начиная от вершины С1 и D1C1=28, то C1Q=12 а QD1=16. Аналогично D1P=16. Найдем PQ
[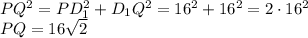
Из прямоугольного треугольника CC1Q найдем CQ
В трапеции опустим высоту QH и найдем ее из прямоугольного треугольника QHD. HD это проекция боковой стороны на большее основание и равно полуразности оснований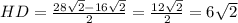
Площадь трапеции равно произведению полусуммы оснований на высоту
ответ